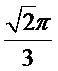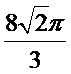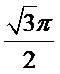棱柱、棱锥、棱台的体积
共114题

· 棱柱、棱锥、棱台的体积

棱柱、棱锥、棱台的体积
共114题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

利用一个球体毛坯切削后得到一个四棱锥P—ABCD，其中底面四边形ABCD是边长为1的正方形，PA=1，且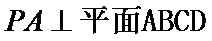，则球体毛坯体积的最小值应为（）

正确答案

解析

由题设知，当所求的球恰为四棱锥的外接球时，球体毛坯体积达到最小值，而此外接球可以与棱长为1的正方体的外接球相同，即，所以，故选D选项。

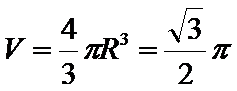
考查方向

本题主要考查了四棱锥的外接球问题，在近几年的各省高考题出现的频率较高，常是独立命题，求体积、表面积，也与函数结合求最值问题。

解题思路

由题设当所求的球恰为四棱锥的外接球时，球体毛坯体积达到最小值，而此外接球可以转化棱长为1的正方体的外接球，进而求出半径，再求出球的体积。

易错点

1、无法把问题转化为求四棱锥的外接球进而思路受阻；

2、不会分析如何求外接球的半径。

知识点

组合几何体的面积、体积问题棱柱、棱锥、棱台的体积

题型：简答题

简答题 · 12 分

如图，在三棱柱中，是等边三角形，,是中点.

22.求证：平面；

23.当三棱锥体积最大时求点到平面的距离.

第(1)小题正确答案及相关解析

正确答案

(略)

解析

连结，交于，连.在三棱柱中，四边形为平行四边形，则,又是中点，∴，而平面，平面，∴平面.

考查方向

线面平行的位置关系，点到平面的距离，体积桥求距离的应用

解题思路

关键是在面DCB1中找线，连结，交于，可证DO//A1B

易错点

确定“三棱锥体积最大时”的条件

第(2)小题正确答案及相关解析

正确答案

解析

设点到平面的距离是，则，而，故当三棱锥体积最大时，，即平面.

由（Ⅰ）知：，所以到平面的距离与到平面的距离相等.

∵平面，平面，∴，

∵是等边三角形，是中点，∴，又，平面，平面，∴平面，∴，由计算得：，所以，设到平面的距离为，由得：，所以到平面的距离是

考查方向

线面平行的位置关系，点到平面的距离，体积桥求距离的应用

解题思路

当三棱锥体积最大时，，即平面，再利用体积桥即可求得点到平面的距离.

易错点

确定“三棱锥体积最大时”的条件

题型：单选题

单选题 · 5 分

11．四棱锥的底面是边长为的正方形，高为1，其外接球半径为，

则正方形的中心与点之间的距离为

正确答案

解析

可求得正方形的对角线长为4，设球心为，则到正方形的中心为，到正方形的距离为1，所以到正方形的中心距离与到球心的距离相等，则为.

A选项不正确，C选项不正确，D选项不正确，所以选B选项。

考查方向

本题主要考查了四棱锥的外接球问题，考察空间想象能力.

解题思路

求出球心到正方形的中心的距离，再结合图形判断位置关系求解.

易错点

球心位置的确定

知识点

棱柱、棱锥、棱台的体积与球体有关的内切、外接问题

题型：填空题

填空题 · 5 分

9．现有橡皮泥制作的底面半径为5，高为4的圆锥和底面半径为2，高为8的圆柱各一个，若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为　　．

正确答案

解析

由题意可知，原来圆锥和圆柱的体积和为：．

设新圆锥和圆柱的底面半径为r，

则新圆锥和圆柱的体积和为：．

∴，解得：．

故答案为：

考查方向

本题考查了圆柱与圆锥的体积公式，是基础的计算题

解题思路

由题意求出原来圆柱和圆锥的体积，设出新的圆柱和圆锥的底面半径r，求出体积，由前后体积相等列式求得r．

易错点

本题考查了圆柱与圆锥的体积公式在计算半径时易错

知识点

棱柱、棱锥、棱台的侧面积和表面积棱柱、棱锥、棱台的体积

题型：单选题

单选题 · 5 分

8.如图，在长方体中，点分别是棱,上的动点，，直线与平面所成的角为，则△的面积的最小值是

D10

正确答案

解析

设直角三棱锥C-C’PQ的高为h, CQ=x,CP=y,根据直角三棱锥的性质可知，+，而直线CC’与平面C’PQ成的角为，所以h=sin=；所以+= ，+ ，所以xy再由体积桥可知：=，=xy ，=xy，所以的最小值为8，选择B.

考查方向

本题主要考查直角三棱锥的重要的性质，直线与平面所成的角。

解题思路

设CQ=x,CP=y, 根据直角三棱锥的性质+，再利用线面角，求出椎体的高h，并应用均值不等式得xy，利用体积桥得=xy，进而求出最小值。

易错点

直角三棱锥的重要性质应用不熟

知识点

棱柱、棱锥、棱台的体积线面角和二面角的求法

继续学习学习下一知识点

下一知识点 : 球的体积和表面积

百度题库 > 高考 > 理科数学 > 棱柱、棱锥、棱台的体积

扫码查看完整答案与解析