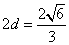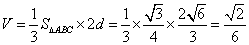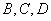- 棱柱、棱锥、棱台的体积
- 共114题
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45。
,AB=2
(1)求证:平面PCD⊥平面PAC;
(2)求直线PB与平面PCD所成角的大小;
(3)求四棱锥P—ACDE的体积。
正确答案
见解析。
解析
(1) 证明 :在
所以
因此 

又 

又 
所以 
所以 
(2)解法一:
因为 三角形
所以 
因此 
又 
所以点B到平面

由于


所以 
故 

所以B到平面平面

设直线


则
又
所以 
解法二:
由(1)知






又
因此 
因为 
所以 四边形
因为 
所以 
因此 
故 
所以 
因此 
设

则 
解得 
取

又
设



则 
所以 
因此直线PB与平面PCD所成角为
(3)因为
所以 四边形四边形
因为 
所以 
因此 
故 
所以 
又 
所以 四棱锥P—ACDE的体积
知识点
已知三棱锥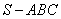
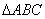

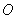
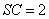
正确答案
解析
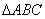
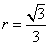
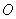
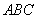
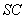
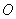
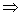
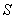
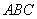
此棱锥的体积为
另:
知识点
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________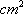
正确答案
24
解析
由已知得此几何体的直观图是一个底面是直角三角形且两直角边分别是3,4高是5的直三棱柱在上面截去一个三棱锥,三棱锥从一个顶点出发的三条棱两两垂直,底面边长分别是3,4高是3,如图3所示,红色为截去的三棱锥,所以体积为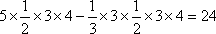
知识点
已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于___________cm3。
正确答案
1
解析
观察三视图知该三棱锥的底面为一直角三角形,右侧面也是一直角三角形,故体积等于
知识点
某几何体的三视图如图所示,则该几何体的体积为( )。
正确答案
解析
由几何体的三视图可得,该几何体是一个横放的直棱柱,棱柱底面为梯形,梯形两底长分别为2和8,高为4,棱柱的高为10,故该几何体体积V=
知识点
扫码查看完整答案与解析