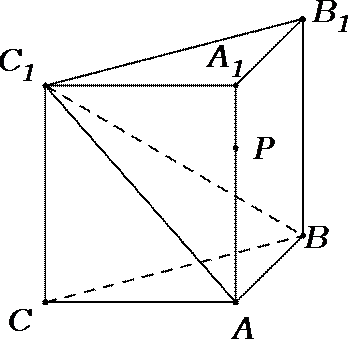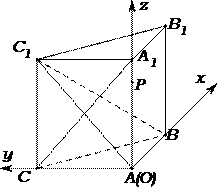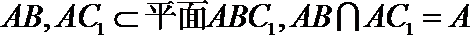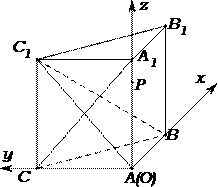- 棱柱、棱锥、棱台的体积
- 共114题
已知四棱锥
(1)求四棱锥
(2)若

求证:

(3)求二面角
正确答案
见解析。
解析
由三视图可知,四棱锥


(1)由锥体体积公式得
(2)连接







所以



(3)以





设面
由

另解:作BG

知识点
19.如图,侧棱垂直底面的三棱柱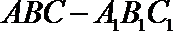
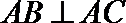
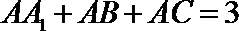
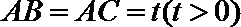
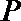
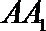
(Ⅰ)当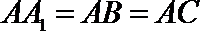
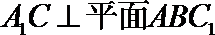
(Ⅱ)试求三棱锥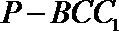
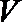
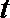
(Ⅲ)若二面角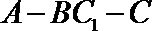
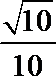
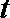
正确答案
(Ⅰ)证法一:∵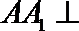
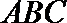
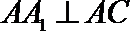
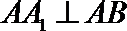
又∵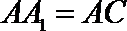
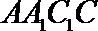
∴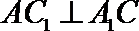
∵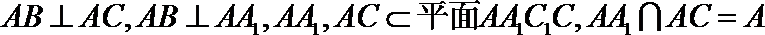
∴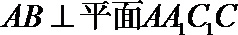
又∵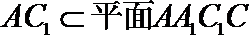
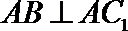
∵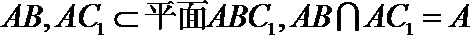
∴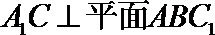
证法二:
∵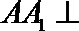
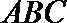
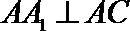
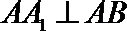
又∵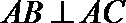
∴分别以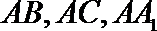
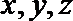
则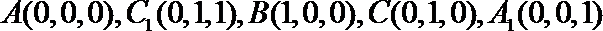
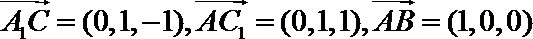
∴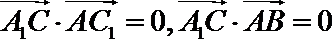
∴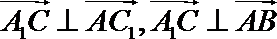
又∵
∴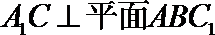
证法三:
∵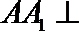
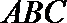
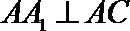
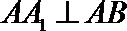
又∵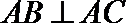
∴分别以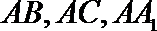
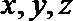
则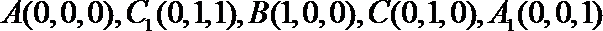
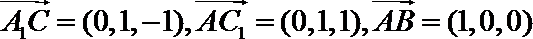
设平面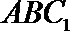
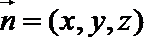
则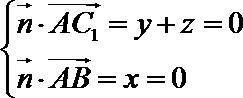
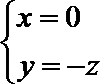
令
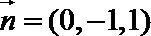
∵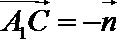
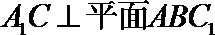
(Ⅱ)∵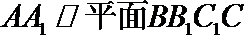
∴点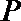
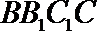
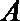
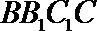
∴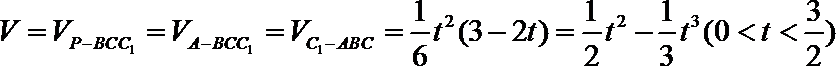
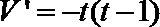
令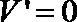
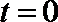
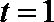
得
∴当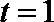
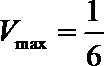
(Ⅲ)
分别以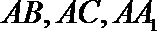
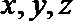
则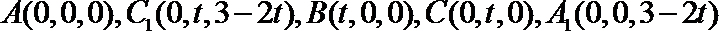
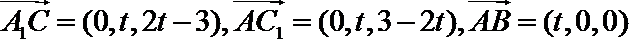
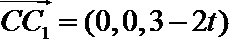
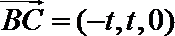
设平面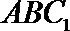
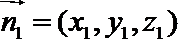
则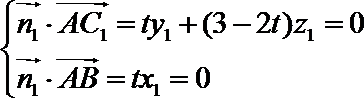
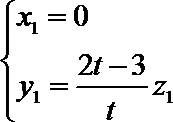
令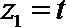
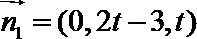
设平面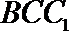
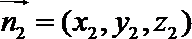
则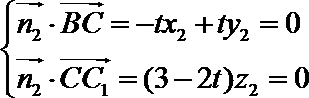
由于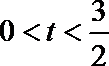
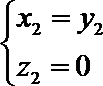
令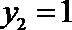
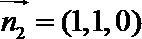
设二面角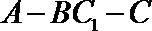
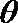
则有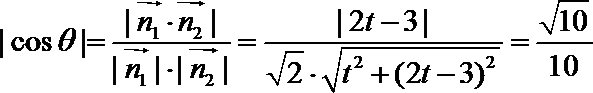
化简得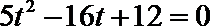
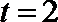
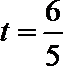
所以当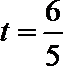
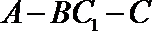
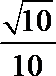
解析
解析已在路上飞奔,马上就到!
知识点
13. 如图,在三棱锥D- ABC中,已知BC丄AD,BC=2 ,AD=6,AB+BD=AC+CD=10,则三棱锥D一ABC的体积的最大值是___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图示,已知平行四边形ABCD和矩形ACEF所在平面互相垂直,AB=1,AD=2,
(1)求证:
(2)设二面角A—FD—B的大小为

(3)设点P为一动点,若点P从M出发,沿棱按照
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析