- 棱柱、棱锥、棱台的体积
- 共114题
19.请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得

(1)若广告商要求包装盒侧面积S(cm

(2)若广告商要求包装盒容积V(cm


正确答案
解:(1)由题意知, 包装盒的底面边长为







(2)包装盒容积V=

所以





所以当



解析
解析已在路上飞奔,马上就到!
知识点
20.已知,如图四棱锥













(1)求异面直线

(2)若



正确答案
解法一:(1)
由已知
∴PG=4
如图所示,以G点为原点建立空间直角坐标系o—xyz,则
B(2,0,0),C(0,2,0),P(0,0,4)
故E(1,1,0)
(2)设F(0,y , z)
在平面PGC内过F点作FM⊥GC,M为垂足,则
解法二:
(1)由已知
∴PG=4
在平面ABCD内,过C点作CH//EG交AD于H,连结PH,则∠PCH(或其补角)就是异面直线GE与PC所成的角.
在△PCH中,
由余弦定理得,cos∠PCH=
(2)在平面ABCD内,过D作DM⊥GC,M为垂足,连结MF,又因为DF⊥GC
∴GC⊥平面MFD, ∴GC⊥FM
由平面PGC⊥平面ABCD,∴FM⊥平面ABCD ∴FM//PG
由GM⊥MD得:GM=GD·cos45°=
解析
解析已在路上飞奔,马上就到!
知识点
18.已知四边形ABCD满足


(1)求四棱锥
(2)证明:
(3)求面
正确答案
(1)取AE的中点M,连结B1M,
因为BA=AD=DC=
则B1M=
所以B1M⊥面AECD,
所以
(2)连结ED交AC于O,连结OF,因为AECD为菱形,OE=OD所以FO∥B1E,
所以
(3)连结MD,则∠AMD=




所以,


设面ECB1的法向量为

令x=1, 


故面

解析
解析已在路上飞奔,马上就到!
知识点
14.已知正三棱柱






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.现有一个关于平面图形的命题:如图所示,同一个平面内的两个边长都是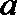
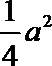
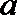
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析