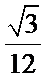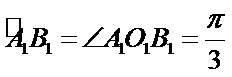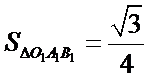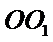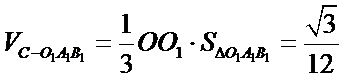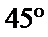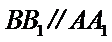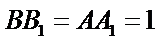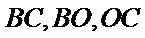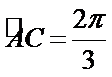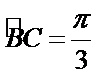- 棱柱、棱锥、棱台的体积
- 共114题
将边长为
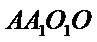
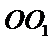
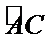
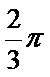
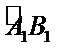
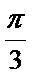
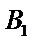
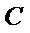
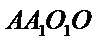
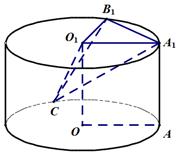
19.求三棱锥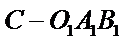
20.求异面直线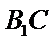
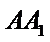
正确答案
解析
连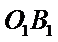
∴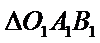
∴
又三棱锥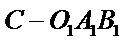
∴
考查方向
解题思路
确定三棱锥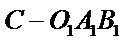
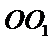
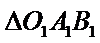

易错点
三棱锥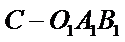
正确答案
解析
设点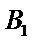
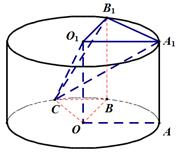
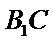
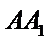
连
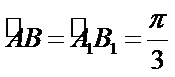
∴
∴
∴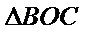
∴
∴
∴
∴直线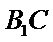
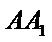
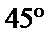
考查方向
解题思路
利用平行,找到直线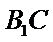
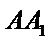
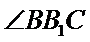
易错点
在圆柱体内找直线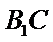
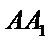
如图4,直三棱柱ABC-A



20.证明:平面AEF⊥平面B

21.若直线A



正确答案
如图,因为三棱柱
所以




所以
解析
见答案
考查方向
解题思路
先证明



易错点
不会证明

正确答案

解析
设AB的中点为D,连接









由题设知,
所以,
在


故三棱锥F-AEC的体积
考查方向
解题思路
设AB的中点为D,证明


由题设知,
易错点
找不到直线与平面所成的角;
17.如图,在四棱锥










(Ⅰ)求证:

(Ⅱ)若



(Ⅲ)当

正确答案
(Ⅲ)四棱锥
解析
(Ⅰ)证明:在平行四边形


所以
由


所以
因为侧面


所以

又因为

所以
又因为




所以

(Ⅱ)证明:因为



所以
又因为






同理,得

又因为




所以平面

又因为

所以

(Ⅲ)解:在




由

又因为
所以
因为

所以

所以四棱锥

考查方向
解题思路
1、第一问由




2、第二问可通过证明平面MEF平行平面PAB得出




3、由PA垂直平面ABCD为基础,通过作PA平行线得出四棱锥






易错点
本题前两问中的证明过程要求严谨、完整,部分学生易书写的不规范、不完整而出错。
知识点
19.如图,四棱锥







(1)求证:


(2)求四棱锥

正确答案
(1)见解析;
(2)
解析
试题分析:本题属于直线与平面垂直的性质、面面垂直的判定、棱锥的体积等知识点的综合应用问题,属于中档题,只要掌握相关的知识,即可解决本题,解析如下:
(1)证明:如图,∵PA⊥底面ABCD,∴PA⊥BC.
又AB⊥BC,PA
又BC
(2)解:∵PA⊥底面ABCD,∴PA⊥AD.
又PC⊥AD,∴AD⊥平面PAC,∴AC⊥AD.
在梯形ABCD中,由AB⊥BC,AB=BC,得
∴
又AC⊥AD,故△DAC为等腰直角三角形,
∴DC=2AB,∴

考查方向
解题思路
(1)先由线面垂直的性质得


(2)易证得


易错点
相关知识点不熟容易证错。
知识点
(4分)(2015•上海)若正三棱柱的所有棱长均为a,且其体积为16
正确答案
4
知识点
扫码查看完整答案与解析