异面直线及其所成的角_章节学习

1

题型：填空题

|

填空题 · 5 分

14. 是两个平面，是两条直线，有下列四个命题：

（1）如果，那么.

（2）如果，那么.

（3）如果，那么.

（4）如果，那么与所成的角和与所成的角相等.

其中正确的命题有． (填写所有正确命题的编号）

正确答案

②③④

解析

试题分析：对于①，，则的位置关系无法确定，故错误；对于②，因为，所以过直线n作平面与平面相交的直线c，则n//c，因为，所以，所以，故②正确；对于③，有两个平面平行的性质可知正确；对于④，由线面所成交的定义和等角定理可知其正确，故正确的有②③④。

考查方向

本题主要考察空间中的线面、面面位置关系等知识点．

解题思路

根据相关定理直接进行判断。

易错点

忽略在空间中考虑线、面关系导致出错。

知识点

异面直线及其所成的角

1

题型：简答题

|

简答题 · 12 分

如图，四边形ABCD为菱形，∠ABC=120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC.

19.证明：平面AEC⊥平面AFC；

20.求直线AE与直线CF所成角的余弦值.

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）（Ⅰ）连接BD，设BD∩AC=G，连接EG，FG，EF，在菱形ABCD中，不妨设GB=1，由∠ABC=120°，可得AG=GC=.

由BE⊥平面ABCD，AB=BC可知，AE=EC，

又∵AE⊥EC，∴EG=，EG⊥AC，

在Rt△EBG中，可得BE=，故DF=.

在Rt△FDG中，可得FG=.

在直角梯形BDFE中，由BD=2，BE=，DF=可得EF=，

∴，∴EG⊥FG，

∵AC∩FG=G，∴EG⊥平面AFC，

∵EG面AEC，∴平面AFC⊥平面AEC.

解析

见答案

考查方向

空间垂直判定与性质；异面直线所成角的计算；空间想象能力，推理论证能力

解题思路

（Ⅰ）连接BD，设BD∩AC=G，连接EG，FG，EF，在菱形ABCD中，不妨设GB=1易证EG⊥AC，通过计算可证EG⊥FG，根据线面垂直判定定理可知EG⊥平面AFC，由面面垂直判定定理知平面AFC⊥平面AEC；

易错点

本题在证明过程中推理不严密易错。

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）

解析

（Ⅱ）如图，以G为坐标原点，分别以的方向为轴，y轴正方向，为单位长度，建立空间直角坐标系G-xyz，由（Ⅰ）可得A（0，－，0），E（1,0, ），F（－1,0，），C（0，，0），∴=（1，，），=（-1，-，）.…10分

故.

所以直线AE与CF所成的角的余弦值为.

考查方向

空间垂直判定与性质；异面直线所成角的计算；空间想象能力，推理论证能力

解题思路

（Ⅱ）以G为坐标原点，分别以的方向为轴，y轴正方向，为单位长度，建立空间直角坐标系G-xyz，利用向量法可求出异面直线AE与CF所成角的余弦值.

易错点

本题在写垂直的过程不能写全条件。

1

题型：简答题

|

简答题 · 14 分

如图2，三角形所在的平面与长方形所在的平面垂直，，，.点是边的中点，点、分别在线段、上，且，.

21.证明：；

22.求二面角的正切值；

23.求直线与直线所成角的余弦值.

第(1)小题正确答案及相关解析

正确答案

（1）见解析；

解析

（1）证明：∵ 且点为的中点，

∴ ，又平面平面，且平面平面，平面，

∴ 平面，又平面，

∴ ；

考查方向

本题考查空间中，面面垂直、线面垂直的相关知识，以及二面角、异面直线所成角等知识，属于中档题．

解题思路

第一问，利用面面垂直的性质定理，可得，于是可证得线线垂直。第二问以及第三问，先找到所求的角，然后利用相关知识算出角即可，也可以建立适当的空间直角坐标系，利用向量法求出角。

易错点

定理的应用不熟练以及建系求角过程中，计算错误。

第(2)小题正确答案及相关解析

正确答案

；

解析

（2）∵ 是矩形，

∴ ，又平面平面，且平面平面，平面，

∴ 平面，又、平面，

∴ ，，

∴ 即为二面角的平面角，

在中，，，，

∴ 即二面角的正切值为；

考查方向

本题考查空间中，面面垂直、线面垂直的相关知识，以及二面角、异面直线所成角等知识，属于中档题．

解题思路

第一问，利用面面垂直的性质定理，可得，于是可证得线线垂直。第二问以及第三问，先找到所求的角，然后利用相关知识算出角即可，也可以建立适当的空间直角坐标系，利用向量法求出角。

易错点

定理的应用不熟练以及建系求角过程中，计算错误。

第(3)小题正确答案及相关解析

正确答案

。

解析

（3）如下图所示，连接，

∵ ，即，

∴ ，

∴ 为直线与直线所成角或其补角，

在中，，，

由余弦定理可得，

∴ 直线与直线所成角的余弦值为．

考查方向

本题考查空间中，面面垂直、线面垂直的相关知识，以及二面角、异面直线所成角等知识，属于中档题．

解题思路

第一问，利用面面垂直的性质定理，可得，于是可证得线线垂直。第二问以及第三问，先找到所求的角，然后利用相关知识算出角即可，也可以建立适当的空间直角坐标系，利用向量法求出角。

易错点

定理的应用不熟练以及建系求角过程中，计算错误。

1

题型：简答题

|

简答题 · 12 分

如图4，直三棱柱ABC-ABC的底面是边长为2的正三角形，E,F分别是BC,CC的中点.

20.证明：平面AEF⊥平面BBCC;

21.若直线AC与平面AABB所成的角为45，求三棱锥F-AEC的体积。

第(1)小题正确答案及相关解析

正确答案

如图，因为三棱柱是直三棱柱，

所以，又E是正三角形的边BC的中点，所以因此，而,

所以.

解析

见答案

考查方向

本题主要考察几何体的体积和面面垂直的判断和性质等知识，意在考察考生的空间向量能力和逻辑推理能力。

解题思路

先证明，得到，由面面垂直的判断定理得到.

易错点

不会证明进而由面面垂直的判断定理得到.

第(2)小题正确答案及相关解析

正确答案

.

解析

设AB的中点为D，连接，因为是正三角形，所以，又三棱柱是直三棱柱，所以，因此CD平面，于是是直线与平面所成的角,

由题设知，

所以，,

在中，,所以，

故三棱锥F-AEC的体积.

考查方向

本题主要考察几何体的体积和面面垂直的判断和性质等知识，意在考察考生的空间向量能力和逻辑推理能力。

解题思路

设AB的中点为D，证明是直线与平面所成的角,

由题设知，求出棱锥的高与底面面积即可求解几何体的体积。.

易错点

找不到直线与平面所成的角；

1

题型：填空题

|

填空题 · 4 分

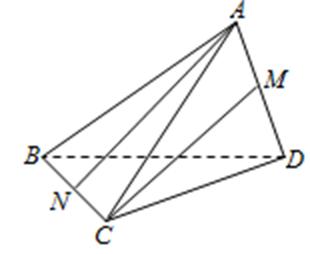
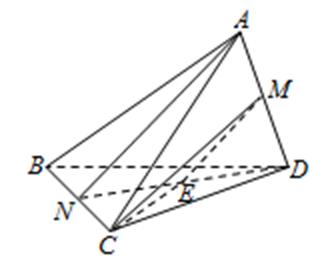
13.如图，三棱锥A-BCD中，AB＝AC＝BD＝CD＝3，AD＝BC＝2，点M,N分别是AD,BC的中点，则异面直线AN，CM所成的角的余弦值是．

正确答案

；

解析

试题分析：利用中位线作出异面直线所成的角，然后在三角形中利用余弦定理求出余弦值即可。

连结ND，取ND 的中点为E，连结ME，则ME∥AN，异面直线AN，CM所成的角就是∠EMC，
∵，∴，
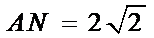
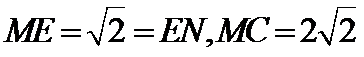
又∵EN⊥NC，∴，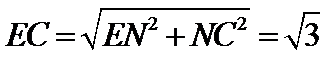

∴．
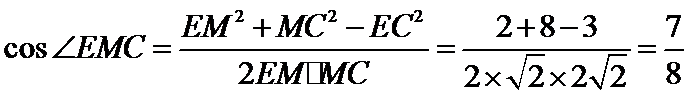
故答案为：．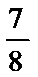

考查方向

本题考查了异面直线所成的角，余弦定理的应用，属于基础题．

解题思路

连结ND，取ND 的中点为E，连结ME说明异面直线AN，CM所成的角

就是∠EMC通过解三角形，求解即可．

易错点

异面直线所成的角为锐角或直角.

知识点

异面直线及其所成的角

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点