圆与圆的位置关系及其判定
共52题

· 圆与圆的位置关系及其判定

圆与圆的位置关系及其判定
共52题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

如图，双曲线的中心在坐标原点，

分别是双曲线虚轴的上、下顶点，是双曲线的左顶点，为双曲线的左焦点，直线与相交于点.若双曲线的离心率为2，则的余弦值是( )

正确答案

解析

略

知识点

圆与圆的位置关系及其判定

题型：填空题

填空题 · 5 分

如图，是⊙的直径，直线切⊙于点，且与延长线交于点，若，，则= 。

正确答案

解析

略

知识点

圆与圆的位置关系及其判定

题型：单选题

单选题 · 13 分

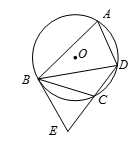
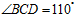
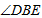
如图，A,B,C,D是⊙O上的四个点，过点B的切线与DC的延长线交于点E.若，则=

正确答案

解析

略

知识点

圆与圆的位置关系及其判定

题型：简答题

简答题 · 12 分

已知函数。

（1）讨论函数在定义域内的极值点的个数；

（2）若函数在处取得极值，对,恒成立，求实数的取值范围；

（3）当，证明：

（4）当且时，试比较的大小，

正确答案

见解析。

解析

（1），当时，在上恒成立，函数在单调递减，∴在上没有极值点；

当时，得，得，

∴在上递减，在上递增，即在处有极小值。

∴当时在上没有极值点，

当时，在上有一个极值点。

（2）∵函数在处取得极值，∴，

∴，

令，可得在上递减，在上递增，

∴，即。

（3）证明：，

令，则只要证明在上单调递增，

又∵，

显然函数在上单调递增。

∴，即，

∴在上单调递增，即，

∴当时，有。

知识点

圆与圆的位置关系及其判定

题型：简答题

简答题 · 12 分

已知

（1）求函数的单调增区间

（2）在中，分别是角的对边，且，求的面积。

正确答案

（1）

（2）

解析

（1）因为==

== …………（3分）

所以函数的单调递增区间是[]（）……………（5分）

（2）因为=，所以,又，所以，从而

在中，∵ ∴1=b2+c2-2bccosA,即1=4-3bc.故bc=1………（10分）

从而S△ABC=…………（12分）

知识点

圆与圆的位置关系及其判定

继续学习学习下一知识点

下一知识点 : 两圆的公切线条数及方程的确定

百度题库 > 高考 > 理科数学 > 圆与圆的位置关系及其判定

扫码查看完整答案与解析