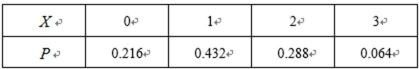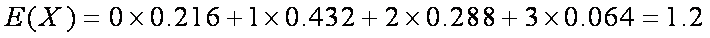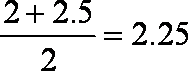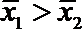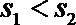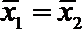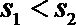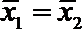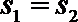- 众数、中位数、平均数
- 共52题
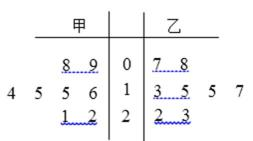
为了从甲乙两人中选一人参加数学竞赛,老师将二人最近6次数学测试的分数进行统计,甲乙两人的平均成绩分别是

正确答案
解析
解:由茎叶图知,
甲的平均数是
乙的平均数是
∴乙的平均数大于甲的平均数,
从茎叶图可以看出乙的成绩比较稳定,
故选D。
知识点
以下五个命题
①从匀速传递的产品生产流水线上,质检员每10分钟0020从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样
②样本方差反映了样本数据与样本平均值的偏离程度
③在回归分析模型中,残差平方和越小,说明模型的拟合效果越好
④在回归直线方程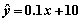
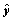
⑤在一个2×2列联表中,由计算得k2=13.079,则其两个变量间有关系的可能性是90%以上.
其中正确的是
正确答案
解析
略
知识点
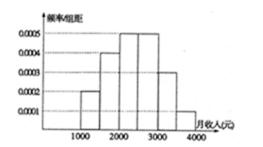
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500) 单位:元)
(1)估计居民月收入在[1500,2000)的概率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)若将频率视为概率,从本地随机抽取3位居民(看作有放回的抽样),求月收入在[2500,3500)的居民数X的分布和数学期望。
正确答案
见解析。
解析
(1)依题意及频率分布直方图知,居民月收入在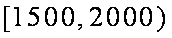
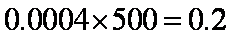
(2)频率分布直方图知,中位数在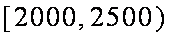
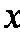
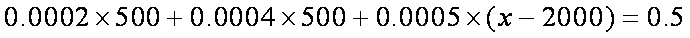
解得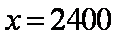
(3)居民月收入在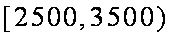
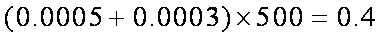
由题意知,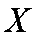
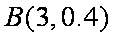
因此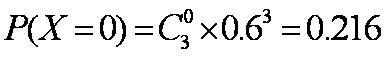
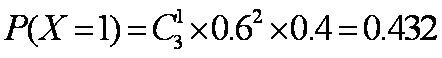
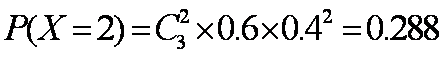
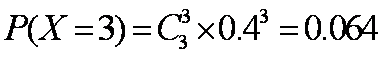
故随机变量X的分布列为
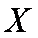
知识点
我国政府对PM2。5采用如下标准:
某市环保局从180天的市区PM2。5监测数据中,随机抽取l0天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)。
(1)求这10天数据的中位数.
(2)从这l0天的数据中任取3天的数据,记

(3)以这10天的PM2。5日均值来估计这180天的空气质量情况,其中大约有多少天的空气质量达到一级。
正确答案
见解析
解析
(1)10天的中位数为(38+44)/2=41(微克/立方米) ·············2分
(2)由 

利用

··············10分
(3)一年中每天空气质量达到一级的概率为



知识点
某航空公司进行空乘人员的招聘,记录了前来应聘的6名男生和9名女生的身高,数据用茎叶图表示如图(单位:cm),应聘者获知:男性身高在区间[174,182],女性身高在区间[164,172]的才能进入招聘的下一环节。
(1)求6名男生的平均身高和9名女生身高的中位数;
(2)现从能进入下一环节的应聘者中抽取2人,记X为抽取到的男生人数,求X的分布列及期望。
正确答案
见解析
解析
(1)6名男生的平均身高为
(2)男性身高在区间[174,182]的有176、178、180;女性身高在区间[164,172]的166,167,168,170,则
X的可能取值为0,1,2,所以
P(X=0)=




X的分布列为
期望为0×


知识点
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中的微量元素
(1)已知甲厂生产的产品共有98件,求乙厂生产的产品数量;
(2)若产品中的微量元素


①用上述样本数据估计乙厂生产的优等品的数量;
②从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数
正确答案
见解析
解析
(1)乙厂生产的产品总数为
(2)显然编号为2,5的产品为优等品,即样本中有两件产品为优等品
所以,样本中优等品的频率为
所以,乙厂生产的优等品的数量为



∴

知识点
右图是2008年北京奥运会上,七位评委为某奥运项目打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数为 ;方差为 .
正确答案
答案:

解析
由茎叶图知,去掉一个最高分93和一个最低分79后,所剩数据84,84,86,84,87的平均数为

知识点
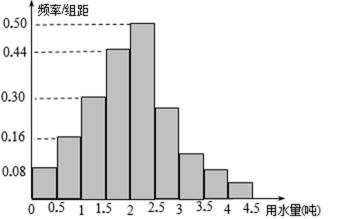
对某小区100户居民的月均用水量进行统计,得到样本的频率分布直方图,则估计此样本的众数、中位数分别为()
正确答案
解析
样本的众数为最高矩形底边中点对应的横坐标,为
中位数是频率为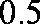
由于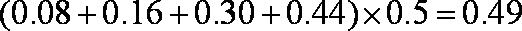
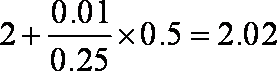
知识点
已知一组正数x1,x2,x3的方差s2=
正确答案
3
解析
由方差的计算公式可得:
S2=



=


=


=

=

可得平均数
对于数据x1+1,x2+1,x3+1的平均数是2+1=3,
故答案为:3。
知识点
4. 甲乙两名运动员在某项测试中的8次成绩如茎叶图所示,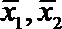
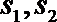
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析