- 极差、方差与标准差
- 共27题
为了解某校学生的视力情况，现采用随机抽样的方式从该校的A，B两班中各抽5名学生进行视力检测，检测的数据如下：
A班5名学生的视力检测结果：4.3，5.1，4.6，4.1，4.9.
B班5名学生的视力检测结果：5.1，4.9，4.0，4.0，4.5.
（1）分别计算两组数据的平均数，从计算结果看，哪个班的学生视力较好？
（2）由数据判断哪个班的5名学生视力方差较大？（结论不要求证明）
（3） 现从A班的上述5名学生中随机选取3名学生，用X表示其中视力大于4.6的人数，求X的分布列和数学期望.
正确答案
解析
（1）解：A班5名学生的视力平均数为
B班5名学生的视力平均数为
从数据结果来看A班学生的视力较好. ……………… 4分
（2）解：B班5名学生视力的方差较大. ……………… 7分
（3）解：由（Ⅰ）知，A班的5名学生中有2名学生视力大于
则
所以 
所以随机变量
……………… 12分
故
知识点
近年来，某市为了促进生活垃圾的风分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应分垃圾箱，为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾，数据统计如下（单位：吨）：
（1）试估计厨余垃圾投放正确的概率；
（2）试估计生活垃圾投放错误额概率；
（3）假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为
（注：
正确答案
（1）
（2）
（3）
解析
（1）由题意可知：
（2）由题意可知：
（3）由题意可知：
知识点
下图是
（注：标准差
A
B
C
D
正确答案
解析
略
知识点
为了从甲乙两人中选一人参加数学竞赛，老师将二人最近6次数学测试的分数进行统计，甲乙两人的平均成绩分别是
A
B
C
D
正确答案
解析
解：由茎叶图知，
甲的平均数是
乙的平均数是
∴乙的平均数大于甲的平均数，
从茎叶图可以看出乙的成绩比较稳定，
故选D。
知识点
样本中共有五个个体，其值分别为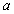
A
B
C
D2
正确答案
解析
由题意知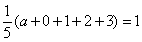
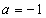
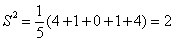
知识点
给出下列四个命题，其中假命题是（ ）
A从匀速传递的新产品生产流水线上，质检员每10分钟从中抽取一件新产品进行某项指标检测，这样的抽样是分层抽样；
B样本方差反映了样本数据与样本平均值的偏离程度；
C在回归分析模型中，残差平方和越小，说明模型的拟合效果越好；
D设随机变量
正确答案
解析
.选项A中的抽样为系统抽样，故此命题为假命题.其它选项为真命题.故选A
知识点
以下五个命题
①从匀速传递的产品生产流水线上，质检员每10分钟0020从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样
②样本方差反映了样本数据与样本平均值的偏离程度
③在回归分析模型中，残差平方和越小，说明模型的拟合效果越好
④在回归直线方程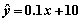
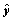
⑤在一个2×2列联表中，由计算得k2=13.079,则其两个变量间有关系的可能性是90%以上.
其中正确的是
正确答案
解析
略
知识点
如图是甲，乙两名同学
正确答案
解析
略
知识点
一种水稻试验品种连续5年的平均单位面积产量(单位：t/hm2)
如下：9.8，9.9，10.1，10，10.2，则该组数据的方差为 。
正确答案
0.02
解析
略
知识点
18.某中学的高二(1)班男同学有
（Ⅰ）求某同学被抽到的概率及课外兴趣小组中男、女同学的人数；
（Ⅱ）经过一个月的学习、讨论，这个兴趣小组决定选出两名同学做某项实验，方法是先从小组里选出
（Ⅲ）试验结束后，第一次做试验的同学得到的试验数据为
正确答案
解：（Ⅰ）
设有
（Ⅱ）把
（Ⅲ）
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析