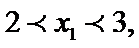- 对数与对数函数
- 共360题
5. 已知点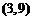
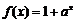

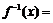
正确答案
解析
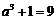
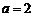
∴
∴
知识点
5.已知点



正确答案
解析
将点


故
∴
∴
∴
考查方向
解题思路
先将点



易错点
对数函数的正确表达形式.
知识点
11.已知函数


正确答案
2.
解析
因为 


考查方向
解题思路
根据函数与反函数的关系可知,因为 


易错点
不理解函数与反函数的关系而出错.
知识点
10.设



正确答案
解析
知识点
12.已知
正确答案
解析
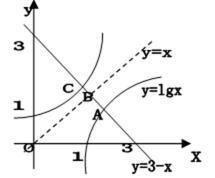
我们首先可以用图象法来解:如图,在同一坐标系中作出四个函数,
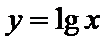
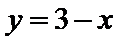

设
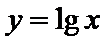
其横坐标为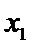
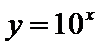
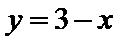
其横坐标为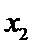
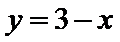

其横坐标为
因为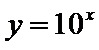
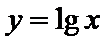

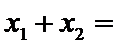
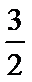
考查方向
解题思路
此属于数形结合法。现在用估计法来解它:因为
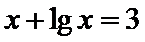
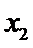
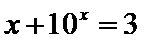
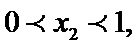
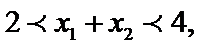
易错点
易忽略函数的对称性,以及指对数函数成反函数的关系
知识点
3.已知函数


正确答案
1
解析
∵



考查方向
本题主要考查了反函数的性质,考查学生分析问题的能力以及计算能力,属于容易题.
解题思路
先求出函数


易错点
求函数


知识点
21.已知函数






正确答案
(1)




(2)不妨设














解析
反函数的应用很重要,学会灵活应用举一反三,导数的应用便于解决实际问题,利用导数求曲线的切线,导数与函数的单调性、最值,比较大小。
考查方向
利用导数求曲线的切线,导数与函数的单调性、最值,比较大小
解题思路







易错点
曲线


知识点
3.已知函数


正确答案
1
解析
因为原函数的函数值与自变量分别是反函数的自变量与函数值,所以原题等价于求

考查方向
解题思路
本题考查反函数的概念以及转化与化归的数学思想,解题思路如下:利用反函数的定义,求

易错点
本题必须注意原函数的函数值与自变量分别是反函数的自变量与函数值,忽视则会出现错误或者导致运算复杂。
知识点
15. 已知函数




函数

正确答案
解析
因为





















考查方向
解题思路
先判断





易错点
①判断函数和反函数的单调性②函数和反函数的图像关系③分析处理问题的能力。
知识点
17. 已知






(1)求

正确答案
解析
因为


且

为





所以
所求的几何体是圆锥挖去同轴的一个圆锥剩下的部分。其体积为
考查方向
解题思路
要找PD在面PAC上的射影,PD和其在面PAC上的射影所成的角即为所求。
根据图形易得所得的几何体是圆锥挖去同轴的一个圆锥剩下的部分,再根据三棱锥的体积公式即可求解。
易错点
不容易找到PD在面PAC上的射影。
(2)求△


①弄清楚所求的几何体的形状②体积公式的正确应用。
知识点
扫码查看完整答案与解析