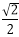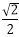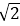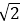- 指数与指数函数
- 共1021题
14.已知函数f(x)是定义在R上的周期为2的奇函数,当0<x<1时,f(x)=,则f()+ f(1)= 。
正确答案
解析
首先,

而

所以:

又

故
考查方向
解题思路
【名师点睛】本题考查函数的奇偶性,周期性,属于基本题,在求值时,只要把


易错点
本题考查函数的奇偶性,周期性,易在奇偶性的应用中发生错误
知识点
4.当


正确答案
解析
假定
则切线方程为
因为过原点,得
而
所以
从而
那么
(1) 当

故函数

(2) 当

故函数

(3) 当
故函数

于是,正确的答案为A.
知识点
3.当0<x≤
正确答案
解析
∵0<x≤
∴0<a<1,排除答案C,D;
取a=

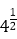
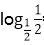
显然4x<logax不成立,排除答案A;故选B
知识点
8.已知函数f(x)=|ex-1|,若a<b<c,且f(a)>f(c)>f(b),则下列结论中必成立的是 .(填序号)
①a<0,b<0,c<0;②a<0,b≥0,c>0;③2-a<2c;④2a+2c<2.
正确答案
解析
画出f(x)的图象如图:
由图象可得a<0,c>0,b在(a,c)之间,但符号不确定,
排除①②,
因为a<0<c,f(a)>f(c),
所以-a>c,
所以2-a>2c,排除③,故选④.
知识点
14.已知




正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数


正确答案
解析
由题可知,x<-1时,f(x)>f(-1)=e,则g(x)的最大值为-1,则m∈
考查方向
解题思路
本题考查函数的图像性质,解题思路如下:画出函数f(x)的图像及g(x)的图像;比较函数值的大小,并求出最大值。
易错点
本题必须注意单调性的比较
知识点
10.已知函数f(x)=x+




f(x1)≥g(x2),则实数a的取值范围是
正确答案
解析
f(x)min=f(1)=5, g(x)min = g(2)=4+a,得a≤1。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
本题主要考查函数的值域
解题思路
1、求出f(x)在[
2、求出f(x)min≥g(x)min,即可得到结果。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在判断范围大小时发生错误。
知识点
13.已知函数


正确答案

考查方向
解题思路
对于分段函数的求值问题,一定要注意自变量

由





易错点
本题忽视分段函数的定义域导致错误。
知识点
正确答案
知识点
12.已知函数


正确答案
解析
令2x=t,(t>0)则当a=0时,y=t,符合题意;当a<0时,函数图像为“对勾函数”,只有a>=1才符合题意;同理,当a>0时,只有当a<=时符合题意。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查函数的性质的综合应用
解题思路
1、对a分类讨论;
2、代入不同的a值,画出函数图像,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易利用指数函数图像时发生错误。
知识点
扫码查看完整答案与解析