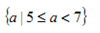- 指数与指数函数
- 共1021题
已知函数

正确答案
解析
知识点
已知点





正确答案
解析
略
知识点
已知函数
(1)当


(3)如果对任意

正确答案
见解析。
解析
(1)当

所以


(2)对函数



当



当



当


则当


故


(3)不妨设
①当




构造函数




当




根据二次函数
所以只需



②当







令

根据二次函数
所以只需



③当



此时





综上所述,实数
知识点
若关于
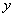
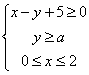
是一个三角形,则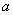
正确答案
解析
略
知识点
下图是某市4月1日至14日的空气质量指数趋势图,空气质量指数小于100
表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机
择4月1日至3月13日中的某一天到达该市,并停留2天.
(1)求此人到达当日空气重度污染的概率;
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
正确答案
见解析
解析
设


根据题意, 

(1)设B为事件“此人到达当日空气重度污染”,则
所以
(2)由题意可知,X的所有可能取值为0,1,2,且
P(X=1)=P(A3∪A6∪A7∪A11)= P(A3)+P(A6)+P(A7)+P(A11)= 
P(X=2)=P(A1∪A2∪A12∪A13)= P(A1)+P(A2)+P(A12)+P(A13)= 
P(X=0)=1-P(X=1)-P(X=2)= 
所以X的分布列为:
故X的期望
(3)从4月5日开始连续三天的空气质量指数方差最大.
知识点
若集合


正确答案
解析
略
知识点
设各项都是正整数的无穷数列



(1)若数列



(2)若

(3)若数列







正确答案
见解析
解析
(1)

(2)根据反证法排除
证明:假设


①当



②当





由①②可知
(3)首先
证明如下:


所以

由题设
即




两式相减得






知识点
若曲线

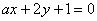

正确答案
解析
略
知识点
一个总体分为甲、乙两层,用分层抽样方法从总体中抽取一个容量为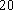

正确答案
180
解析
略
知识点
设函数
(1)若

(2)若函数


(3)过坐标原点


正确答案
见解析
解析
(1)






(2)




即



令

易知



(3)设切点为

切线的斜率



存在性:

所以,

再证唯一性:设




所以方程
综上,切点的横坐标为
知识点
扫码查看完整答案与解析