- 指数与指数函数
- 共1021题
已知函数


(1)求
(2)若
(3)讨论关于x的方程
正确答案
见解析
解析
(1)∵f(x)是定义在R上的奇函数,∴f(0)=0.



则



∴在(0,e)上为增函数,在(e,+∞)上为减函数;
当x=e时,
∴当





知识点
已知数列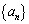

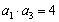


正确答案
解析
略
知识点
已知函数
(1)求函数
(2)求证:存在

(3)对于函数








正确答案
见解析。
解析
(1)
令
令

∴函数

所以

(2)由(1)知

令
∴
取

故存在


………………………………………………(7分)
(说明:


(3)设
则
则当


当


∴

∴
∴函数



设


令函数
①由



即

∴
即
∴

②下面说明:
即
设
则
∵当


当


∴当


∴
综合①②知
故函数


此时
知识点
已知一圆柱内接于球O,且圆柱的底面直径与母线长均为2,则球为O的表面积为 。
正确答案
解析
圆柱的底面直径与母线长均为2,所以球的直径


知识点
已知





正确答案
解析
略
知识点
函数
正确答案
(0,4]
解析
要使函数有意义,必有
所以

故答案为:(0,4]
知识点
某市甲、乙两校高二级学生分别有1100人和1000人,为了解两校全体高二级学生期 末统考的数学成绩情况,采用分层抽样方法从这两所学校共抽取105名高二学生的数学 成绩,并得到成绩频数分布表如下,规定考试成绩在[120,150]为优秀.
甲校:
乙校:
(1) 求表中

(2) 由以上统计数据完成下面2x2列联表,问是否有99%的把握认为学生数学成绩优秀 与所在学校有关?
(3) 若以样本的频率作为概率,现从乙校总体中任取 3人(每次抽取看作是独立重复的),求优秀学生人数
正确答案
见解析。
解析
(1)甲校抽取:

(2)

(3)由题知,乙校优秀的概率是



数列期望为
知识点
已知函数f(x)=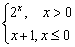
正确答案
解析
略
知识点
设函数y=-3+log2(x-1)(x≥5),则其反函数的定义域为 ________ 。
正确答案
解析
略
知识点
如图,在四棱锥





(1)点





(2)在(I)的条件下,若平面

正确答案
(1)
解析
(1)当

证明:连



由



若

由



(2)由PA=PD=AD=2, Q为AD的中点,则PQ⊥AD
又平面PAD⊥平面ABCD,所以PQ⊥平面ABCD,连BD,
∵四边形ABCD为菱形,∴AD=AB, 由 ∠BAD=60°得△ABD为正三角形,
又∵Q为AD中点, ∴AD⊥BQ ……8分
以Q为坐标原点,分别以QA、QB、QP所在的直线为

设平面MQB的法向量为
可得
令z=1,解得
取平面ABCD的法向量

则

知识点
扫码查看完整答案与解析
































