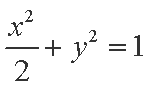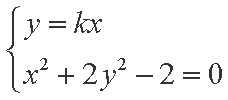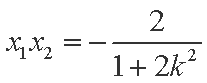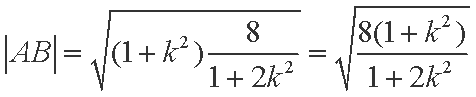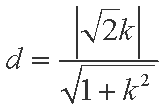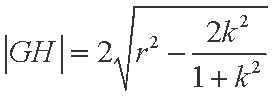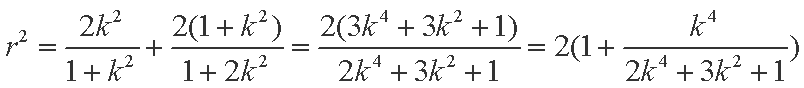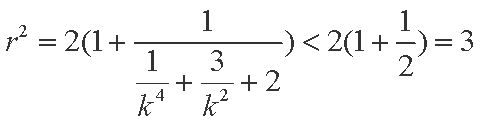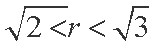- 指数与指数函数
- 共1021题
已知抛物线C:
(1) 若
(2)问在抛物线C上是否存在定点N(x0,y0),使得NA⊥NB总成立,若存在,求出N点的坐标,若不存在,请说明理由
正确答案
见解析
解析
(1)当



则






(2)设在抛物线上存在定点

















由此可得:①当




知识点
已知函数



正确答案
解析
略
知识点
设公比大于零的等比数列










(1)求数列

(2)设


正确答案
见解析
解析
(1)由


又

则得
所以

(2)


则

即

当



知识点
设



(1)求实数

(2)设



(3)若正实数







正确答案
见解析
解析
本题考查运用导数知识研究函数的图象与性质、函数的应用、不等式问题、数学归纳法等基础知识,考查运算求解能力、推理论证能力,考查数形结合思想、函数与方程思想、特殊与一般思想等.
(1)∵


令



所以


(2)由

令函数





而

所以
(3)证明:不妨设

其中

令









从而有
该不等式能更进一步推广:
已知




下面用数学归纳法加以证明:
i)当
ii)假设当

则当



在该不等式的两边同时乘以正数

在此不等式的两边同时加上

该不等式的左边再利用i)的结论可得:

所以,当
综上,对
知识点
若不等式组


正确答案
解析
略
知识点
设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(M⊆D)有x+l∈D,且f(x+l)≥f(x),则称f(x)为M上的l高调函数,如果定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,且f(x)为R上的8高调函数,那么实数a的取值范围是
正确答案
解析
当a=0时,f(x)=x,则f(x+8)>f(x),即f(x)为R上的8高调函数;当a≠0时,函数y=f(x)的图象如图所示,若f(x)为R上的8高调函数,则3a2-(-a2)≤8,解得-≤a≤且a≠0.综上-≤a≤.
知识点
已知函数f (x) =x2, g(x) =2eln x(x>0) (e为自然对数的底数)。
(1)求F(x) =f(x)-g(x) (x>0)的单调区间及最小值;
(2)是否存在一次函数y=kx+b(k,b
正确答案
见解析
解析
(1)
令F′(x)=0,得
∴当0<x<

当x>

∴当x=
即F(x)min=F(

∴F(x)的单调递增区间为(

(2)由(1)知,f(x)与g(x)的图象有且仅有一个公共点(
∴猜想:一次函数的图象就是f(x)与g(x)的图象在点(
其方程为y=2
下面证明:当x>0时,f(x)≥2

∵f(x)-(2


又令G(x)=2


∴当0<x<

当x>

∴当x=
即G(x)min=G(


故存在一次函数y=2


知识点
已知

(1)试利用基本不等式求

(2)若实数


正确答案
见解析
解析
本小题主要考查基本不等式、柯西不等式等基础知识,考查推理论证能力, 考查化归与转化思想。
(1)由三个数的均值不等式得:
(当且仅当


(2)
(当且仅当

整理得:

知识点
设函数
(1)求
(2)若


正确答案
见解析
解析
(1)设函数



(2)∵
∴
∴
知识点
已知圆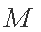
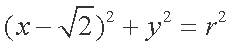


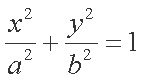

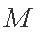
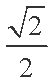
(1)求椭圆
(2)若存在直线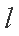
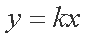

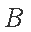
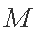

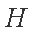

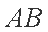
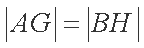
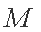
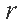
正确答案
见解析
解析
(1)设椭圆的焦距为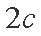
因为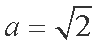
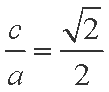
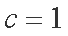
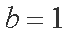

(2)设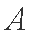

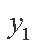
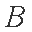
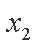
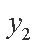
由直线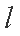

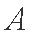
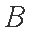
所以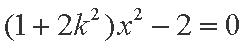

所以
点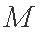
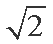
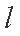
则
显然,若点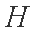
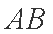
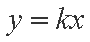
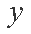
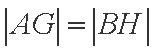
所以
当

当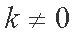
又显然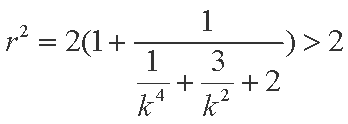
综上,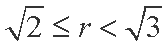
知识点
扫码查看完整答案与解析