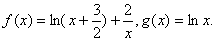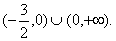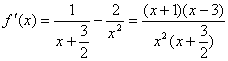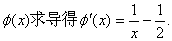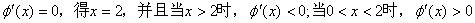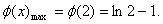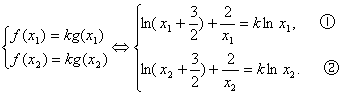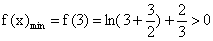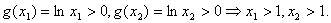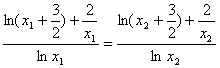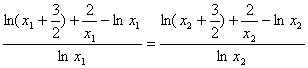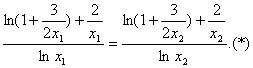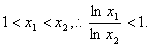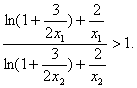指数与指数函数
共1021题

指数与指数函数
共1021题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

若将边长为的正方形绕其一条边所在直线旋转一周，则所形成圆柱的体积等于 .

正确答案

解析

略

知识点

指数函数的图像与性质

题型：单选题

单选题 · 5 分

设，则（）。

正确答案

B,C,D

解析

略

知识点

指数函数的图像与性质对数值大小的比较不等式的性质

题型：单选题

单选题 · 5 分

复数在复平面内的对应点到原点的距离为

正确答案

解析

对应点为

知识点

指数函数的图像与性质

题型：简答题

简答题 · 14 分

已知函数

（1）求函数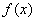的单调区间；

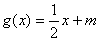
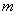
（2）如果关于x的方程有实数根，求实数的取值集合；

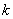
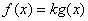
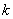
（3）是否存在正数，使得关于x的方程有两个不相等的实数根？如果存在，求满足的条件；如果不存在，说明理由.

正确答案

见解析。

解析

（1）函数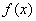的定义域是

对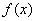求导得

由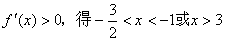，由

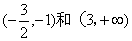
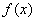
因此是函数的增区间；

（－1，0）和（0，3）是函数的减区间

（2）因为

所以实数m的取值范围就是函数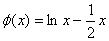的值域

对

令

∴当x=2时取得最大值，且

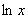
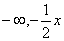
又当x无限趋近于0时，无限趋近于无限趋近于0，

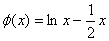
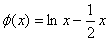
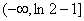
进而有无限趋近于－∞.因此函数的值域是 ,即实数m的取值范围是

（3）结论：这样的正数k不存在。

下面采用反证法来证明：假设存在正数k，使得关于x的方程

有两个不相等的实数根，则

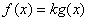
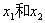
根据对数函数定义域知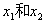都是正数。

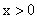
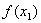
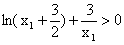
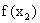
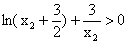
又由（1）可知，当时，

∴=，=，

再由k>0，可得

由于不妨设，

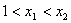
由①和②可得

利用比例性质得

即

由于上的恒正增函数，且

又上的恒正减函数，且∴

∴，这与（*）式矛盾。

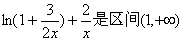
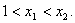
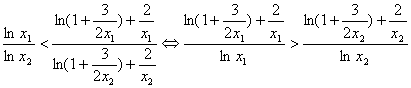
因此满足条件的正数k不存在

知识点

指数函数的图像与性质

题型：单选题

单选题 · 5 分

对于任意两个正整数，定义某种运算“※”，法则如下：当都是正奇数时，※=；

当不全为正奇数时，※=。则在此定义下，集合

中的元素个数是

B11

C13

D14

正确答案

解析

略

知识点

指数函数的图像与性质

题型：单选题

单选题 · 5 分

如图，边长为1的正方形的顶点,分别在轴、轴正半轴上移动，则的最大值是（）

正确答案

解析

略

知识点

指数函数的图像与性质

题型：单选题

单选题 · 5 分

已知e是自然对数的底数，函数的零点为a，函数的零点为b，则下列不等式中成立的是

正确答案

解析

略

知识点

指数函数的图像与性质对数函数的图像与性质函数零点的判断和求解

题型：单选题

单选题 · 5 分

若函数，

正确答案

解析

略

知识点

指数函数的图像与性质

题型：单选题

单选题 · 5 分

已知，满足，则的最大值是

正确答案

解析

由，得，因为，所以。所以，当且仅当，即，时，取等号，所以的最大值是，所以选B.

知识点

指数函数的图像与性质

题型：简答题

简答题 · 13 分

已知：函数，.

（1）求证：函数的图象关于点中心对称，并求的值.

（2）设，，，且，

求证：①请用数学归纳法证明：当时，；

②

正确答案

见解析

解析

解析：（1）设是函数的图象上的任一点，则，

又关于的对称点是，（1分）

而

，即，（3分）

点也在函数的图象上，故的图象关于点中心对称.

（4分）

由于，

R.……，

又.

…………，

，.

故. （6分）

（2）.

①下面用数学归纳法证明：

当时，

假设时，则，又在上单调递减，，这说明时，命题也成立.

由可知. （10分）

②，

由于，，，

于是…….

（12分）

所以，…….

（13分）

知识点

指数函数的图像与性质

继续学习学习下一知识点

下一知识点 : 对数与对数函数

百度题库 > 高考 > 理科数学 > 指数与指数函数

扫码查看完整答案与解析