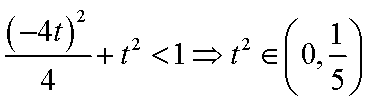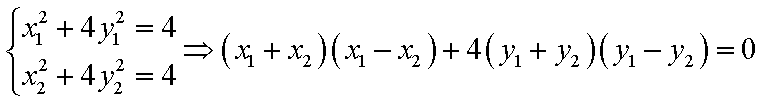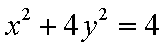- 指数与指数函数
- 共1021题
已知函数




①函数


②函数

③如果当


④当


⑤函数
其中正确命题的序号是 。
正确答案
①②⑤
解析
由导数图象可知,当



























知识点
某汽车驾驶学校在学员结业前,对学员的驾驶技术进行4次考核,规定:按顺序考核,一旦考核合格就不必参加以后的考核,否则还需参加下次考核。若学员小李独立参加每次考核合格的概率依次组成一个公差为


(1)求小李第一次参加考核就合格的概率
(2)求小李参加考核的次数
正确答案
见解析
解析
解析:(1)根据题意,得 


∵


(2)由(1)的结论知,小李四次考核每次合格的概率依次为
∴



∴小李参加测试的次数

知识点
已知函数


正确答案
答案:
解析
略
知识点
已知函数








(1)求

(2)若点




正确答案
见解析
解析
(1)
所以




(2)设点




连接

又因为

在

解得



知识点
设函数





(1)求

(2)若数列


(3)如果




正确答案
见解析。
解析
由

(1)令

∴
若

∴






∴函数

(2)
由函数


得到数列

∴

(3)当
∴



可以得出数列


∴数列


知识点
一笼子中装有2只白猫,3只黑猫,笼门打开每次出来一只猫,每次每只猫都有可能出来。
(1)第三次出来的是只白猫的概率;
(2)记白猫出来完时笼中所剩黑猫数为

正确答案
见解析。
解析
(1)所有可能情况为


(2)设笼中所剩黑猫数为





其概率分布列如下:
知识点
已知




(1)过坐标原点



(2)令



正确答案
见解析
解析
(1)

所以切线的斜率
整理得
显然,


所以方程

(2)

设

易知


①当











所以,
②当



则




又∵
∴


当



从而



∴
综合①②得,
知识点
“中国式过马路”一经网络传播,立刻引发广大群众对交通、国民素质和安全意识的讨论,某班的数学课外探究小组决定对“中国式过马路”现象做一次探究活动,于星期日在某交通岗进行了30分钟的行人过岗是否“闯红灯”的调查,将调查的结果统计成诸多的统计表,其中的两个统计表如下:
表1:过岗人员统计表
表2:过岗人员中的学生情况统计表
根据以上所给信息,回答下列问题:
(1)你是否有95%的把握认为某人过交通岗是否闯红灯与其性别有关?并说明你的理由;
(2)对调查过程中通过交通岗的学生都进行了简单的问卷调查,现在从女学生的问卷中任意抽取4份进行分析,考虑到分析的科学性,要求中学女生数不小于小学女生数,设小学女生问卷被抽取的份数为


附:
正确答案
见解析
解析
(1)有95%的把握认为某人过交通岗是否闯红灯与其性别有关
由表1及

因为
(2) 由表2及题意得



即分布列为
所以

知识点
在直角坐标系







(1)求曲线

(2)求曲线

正确答案
(1)C1:x2+(y-1)2=1,C2:x-y+1=0
(2)1
解析
(1)将


将

(2) 由(1)知曲线






知识点
椭圆C的两焦点坐标是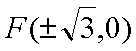
(1)求椭圆C的方程;
(2)已知点N的坐标为

正确答案
见解析
解析
(1)椭圆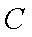

(2)由题意设
设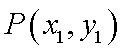
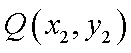
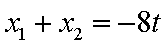
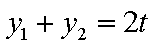
由题意得:
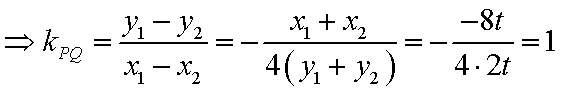
设直线
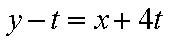
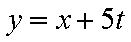
得:
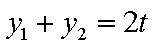
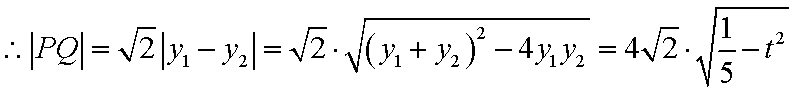
点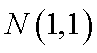
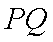
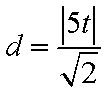
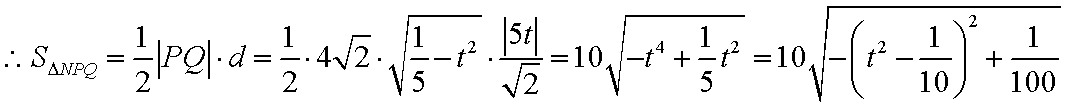
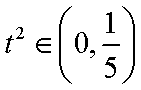
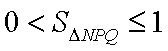
即:
知识点
扫码查看完整答案与解析