- 立体几何与空间向量
- 共3353题
17.已知如图,四边形ABCD是直角梯形,AD//BC,CD⊥AD,PA⊥平面ABCD,
(1)求证:BD//平面AEF;
(2)求点A到平面PBC的距离。
正确答案
见解析。
解析
(1)证明:连接BD,因为E、F分别是PB、PD的中点.在

(2)设A到平面PBC的距离为d,因为




知识点
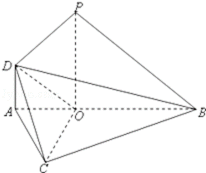
18.如图,在△ABC中,已知∠ABC=45°,O在AB上,且OB=OC=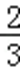
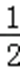
(1)求证:PD⊥平面COD;
(2)求二面角B﹣DC﹣O的余弦值。
正确答案
见解析。
解析
(1)证明:设OA=1,则PO=OB=2,DA=1,
由DA∥PO,PO⊥平面ABC,知DA⊥平面ABC,
∴DA⊥AO,从而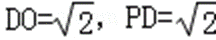
在△PDO中,∵PO=2,
∴△PDO为直角三角形,故PD⊥DO。
又∵OC=OB=2,∠ABC=45°,
∴CO⊥AB,又PO⊥平面ABC,
∴PO⊥OC,
又PO,AB⊂平面PAB,PO∩AB=O,
∴CO⊥平面PAB。
故CO⊥PD。
∵CO∩DO=O,
∴PD⊥平面COD。
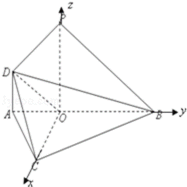
(2)解:以OC,OB,OP所在射线分别为x,y,z轴,建立直角坐标系如图。
则由(1)知,C(2,0,0),B(0,2,0),P(0,0,2),D(0,﹣1,1),
∴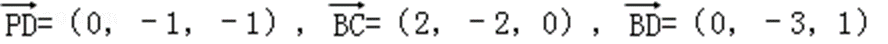
由(1)知PD⊥平面COD,∴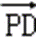
设平面BDC的法向量为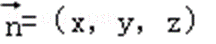
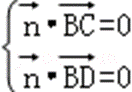
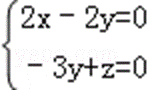
令y=1,则x=1,z=3,∴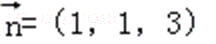
∴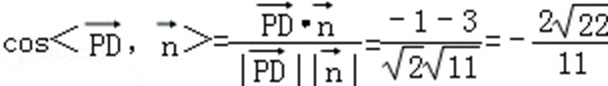
由图可知:二面角B﹣DC﹣O为锐角,二面角B﹣DC﹣O的余弦值为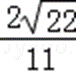
知识点
15.如图,⊙










正确答案
解析
略。
知识点
18.如图1,在直角梯形









(1)求证:
(2) 求

(3)判断直线

正确答案
见解析。
解析
(1)
证明:因为 四边形
所以 
因为 平面





所以 

因为 

所以 
(2)如图,以点



设

所以 


设平面

由
令


设


则
所以 


(3)
直线

由题意得,
所以 
所以 
因为 

所以 
另解:直线

取






所以 

因为 


所以 

所以 

所以 
所以 

因为 四边形

所以 


所以 



所以 


知识点
14.直线l的参数方程是

正确答案
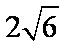
解析
略。
知识点
12.已知




正确答案
解析
以共顶点,长度为1的两个线段为领边作平行四边形,考虑从此顶点出发的对角的长度,易得在夹角为



知识点
4.某几何体的三视图如下图所示,则该几何体的表面积为( )
正确答案
解析
由三视图可知几何体为下部是底面半径为3,高为6的圆柱,上部是侧棱长为5,底面边长为





知识点
2.某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则其侧视图的面积是( )
正确答案
解析
略。
知识点
3.设随机变量X服从正态分布

正确答案
解析
略。
知识点
6.如图, 一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积为( )
正确答案
解析
由题意,棱锥的高为


知识点
9.已知点







正确答案
解析
与平面



知识点
某音乐喷泉喷射的水珠呈抛物线形,它在每分钟内随时间






(1)试求此喷泉喷射的圆形范围的半径最大值;
(2)若在一建筑物前计划修建一个矩形花坛并在花坛内装置两个这样的喷泉,则如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?
正确答案
见解析。
解析
(1)当
因


从而当


所以此喷泉喷射的圆形范围的半径最大值是
(2)设花坛的长、宽分别为xm,ym,根据要求,矩形花坛应在喷水区域内,顶点应恰好位于喷水区域的边界,依题意得:

问题转化为在


法一:





法二:∵


∴当




答:花坛的长为

知识点
11.(a+x)4的展开式中x3的系数等于8,则实数a=_________。
正确答案
2
解析
知识点
12.若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于()
正确答案
解析
由正视图知:三棱柱是以底面边长为2,高为1的正三棱柱,所以底面积为

知识点
20.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的周期为π,图象的一个对称中心为

(1)求函数f(x)与g(x)的解析式;
(2)是否存在x0∈
(3)求实数a与正整数n,使得F(x)=f(x)+ag(x)在(0,nπ)内恰有2 013个零点。
正确答案
见解析。
解析
(1)由函数f(x)=sin(ωx+φ)的周期为π,ω>0,得ω=
又曲线y=f(x)的一个对称中心为
故

将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得y=cos x的图象,再将y=cos x的图象向右平移

(2)当x∈



所以sin x>cos 2x>sin xcos 2x.
问题转化为方程2cos 2x=sin x+sin xcos 2x在
设G(x)=sin x+sin xcos 2x-2cos 2x,x∈
则G′(x)=cos x+cos xcos 2x+2sin 2x(2-sin x)。
因为x∈

又

且函数G(x)的图象连续不断,故可知函数G(x)在
即存在唯一的x0∈
(3)依题意,F(x)=asin x+cos 2x,令F(x)=asin x+cos 2x=0.
当sin x=0,即x=kπ(k∈Z)时,cos 2x=1,从而x=kπ(k∈Z)不是方程F(x)=0的解,
所以方程F(x)=0等价于关于x的方程

令
则问题转化为研究直线y=a与曲线y=h(x),x∈(0,π)∪(π,2π)的交点情况。



当x变化时,h′(x),h(x)的变化情况如下表:
当x>0且x趋近于0时,h(x)趋向于-∞,
当x<π且x趋近于π时,h(x)趋向于-∞,
当x>π且x趋近于π时,h(x)趋向于+∞,
当x<2π且x趋近于2π时,h(x)趋向于+∞。
故当a>1时,直线y=a与曲线y=h(x)在(0,π)内无交点,在(π,2π)内有2个交点;
当a<-1时,直线y=a与曲线y=h(x)在(0,π)内有2个交点,在(π,2π)内无交点;
当-1<a<1时,直线y=a与曲线y=h(x)在(0,π)内有2个交点,在(π,2π)内有2个交点。
由函数h(x)的周期性,可知当a≠±1时,直线y=a与曲线y=h(x)在(0,nπ)内总有偶数个交点,从而不存在正整数n,使得直线y=a与曲线y=h(x)在(0,nπ)内恰有2 013个交点;
又当a=1或a=-1时,直线y=a与曲线y=h(x)在(0,π)∪(π,2π)内有3个交点,由周期性,2 013=3×671,所以依题意得n=671×2=1 342.
综上,当a=1,n=1 342或a=-1,n=1 342时,函数F(x)=f(x)+ag(x)在(0,nπ)内恰有2 013个零点。
知识点
扫码查看完整答案与解析