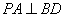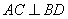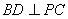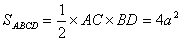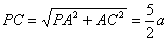- 平面与平面垂直的判定与性质
- 共129题
如图,在四棱锥








(1)求证:
(2)求证:平面

(3)在




正确答案
见解析
解析
(1)证明:因为△



因为平面



所以

因为


(2)证明:因为




因为



因为


因为



(3)存在点



证明:因为



因为





同理可得

因为


知识点
如图4,四棱锥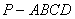
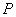
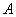
(1)求证: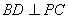
(2)若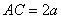
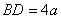
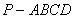
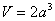
正确答案
见解析。
解析
(1)依题意,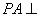
因为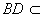
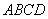
依题意,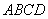
因为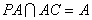
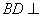
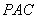
⑵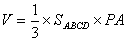
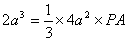
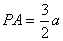
知识点
如图3,在四棱锥
(1)求证:BG平面PAD;
(2)求三棱锥G—CDP的体积;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF平面ABCD,并证明你的结论.
正确答案
见解析。
解析
证明:连结BD.
因为ABCD为棱形,且∠DAB=60°,所以ABD为正三角形.
又G为AD的中点,所以BG⊥AD.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD.
(2)因为G为正三角形PAD的边AD的中点,所以PGAD.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
所以PG⊥平面ABCD.
因为正三角形PAD的边长为2,所以
在CDG中,CD=2,DG=1,∠CDG=120°,
所以
故
(3)当F为PC的中点时,平面DEF⊥平面ABCD.
取PC的中点F,连结DE,EF,DF,CG,且DE与CG相交于H.
因为E、G分别为BC、AD的中点,所以四边形CDGE为平行四边形.
故H为CG的中点. 又F为CP的中点,所以FH//PG.
由(2),得PG平面ABCD,所以FH平面ABCD.
又FH平面DEF,所以平面DEF⊥平面ABCD.
知识点
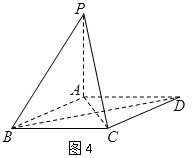
如图,已知三棱锥A—BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形。
(1)求证:DM//平面APC;
(2)求 证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D—BCM的体积。
正确答案
见解析。
解析
知识点
如图1,在Rt△ABC中,∠ABC=90°,D为AC中点,




(1)若M是FC的中点,求证:直线

(2)求证:BD⊥
(3)若平面


正确答案
见解析
解析
(1)因为




又
所以
(2)因为

所以
又
所以
(3)直线

因为



所以 
因为

又因为

假设
因为

所以
所以
这与
所以直线

知识点
已知直线
正确答案
解析
略
知识点
设a,b,c是空间三条直线,
正确答案
解析
略
知识点
设

正确答案
解析
略
知识点
如图,正方形ADEF所在平面和等腰梯形所在平面ABCD垂直,已知BC=2AD=4,
(1)
(2)求异面直线BE与AF所成的角;
(3)求该几何体的表面积。
正确答案
见解析。
解析
知识点
三棱锥







正确答案
解析
在△




















知识点
扫码查看完整答案与解析