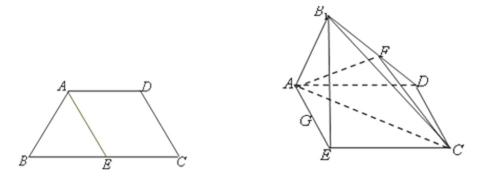
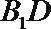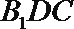- 平面与平面垂直的判定与性质
- 共129题
如图,正方形


(1)求证:
(2)求多面体
正确答案
见解析
解析
本题主要考查空间线与线、线与面的位置关系、体积的计算等基础知识;考查空间想象能力、运算求解能力及推理论证能力。
(1)证明:









(2)设






∴



即多面体

知识点
如图,四棱锥


(1)平面PAD与平面PAB是否垂直?并说明理由;
(2)求直线PC与平面ABCD所成角的正弦值。
正确答案
见解析。
解析
(1)平面
∵
∵四棱锥

∵






∵




平面

(2)如图,过点




由(1)可知
∵
∴平面
∵



平面

∴
∴


∴






在直角三角形
故
在直角三角形

故直线


知识点
19.如图,已知 DE⊥平面 ACD , DE / / AB , △ ACD 是正三角形, AD = DE 
(1)求证:AF //平面 BCE ;
(2)求证:平面 BCE ⊥平面 CDE .
(3)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,







(1)求证:
(2)设


(3)设平面


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设

①若



②若




③设



④直线


其中所有的真命题的序号是__________ .
正确答案
①②
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,







(1)求证:
(2)设


(3)设平面


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知四边形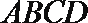
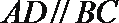
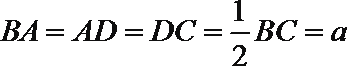
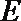
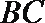
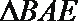
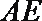
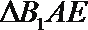
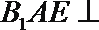
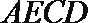
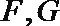
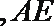
(Ⅰ)求三棱锥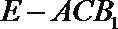
(Ⅱ)证明:平面
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设m,n是不同的直线,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,已知四棱锥







(1)求证:
(2)求 四棱锥
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,已知矩形













(1)求证:平面


(2)设





正确答案
(1)证明:
(2)
如图,建立坐标系,则

易知
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析