- 函数解析式的求解及常用方法
- 共158题
某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:由下表可得回归直线方程为
正确答案
49
解析
略
知识点
某公司生产电饭煲,每年需投入固定成本40万元,每生产1万件还需另投入16万元的变动成本,设该公司一年内共生产电饭煲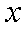
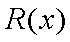
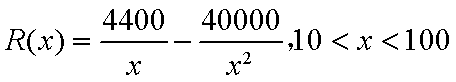
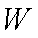
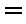
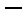
(1)写出年利润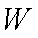
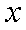
(2)为了让年利润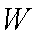
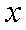
正确答案
见解析
解析
(1)
(2) 解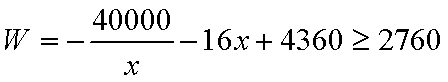
得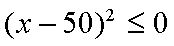
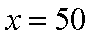
答:为了让年利润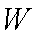
知识点
已知f(x)=mlnx﹣
(1)求函数f(x)的单调区间;
(2)当m=


正确答案
见解析。
解析
(1)f′(x)=
当m≤0时,f′(x)≤0,此时函数在(0,+∞)单调递减。
当m>0时,由f′(x)=0,解得x=2m。
令f′(x)>0,解得0<x<2m,此时函数f(x)单调递增;令f′(x)<0,解得2m<x,此时函数f(x)单调递减。
∴函数f(x)的单调递增区间为(0,2m),单调递减区间为(2m,+∞)。
(2)对于任意x1∈[

当m=


当x∈[1,e]时,函数f(x)单调递减。
∴当x=1时,函数f(x)取得最大值,f(x)max=f(1)=﹣
当x∈
g(x)=2cos2x+sinx+a=2(1﹣sin2x)+sinx+a=-2sin2x+sinx+2+a=
∴当sinx=


∴

∴实数a的取值范围是
知识点
由于受大气污染的影响,某工程机械的使用年限x(年)与所支出的维修费用
假设
(1)求维修费用
(2)使用年限为8年时,维修费用大概是多少?
参考公式:回归方程

正确答案
见解析
解析
解析:(1)




所以

故线性回归方程为
(2)将x=8,代入回归方程得

知识点
在平面直角坐标系下,已知



(1)求
(2)求
正确答案
见解析
解析
(1)依题意得
∴

(2) 由(1)得



∴
∴


知识点
扫码查看完整答案与解析