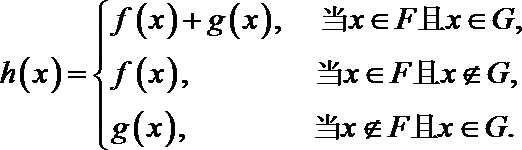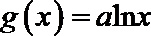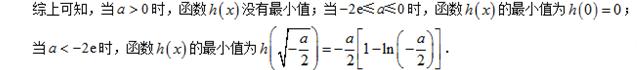- 函数解析式的求解及常用方法
- 共158题
已知函数
(1)当

(2)当


的区域内,求
正确答案
见解析
解析
(1)

①当
②当
所以函数的单调递增区间是

(2)由题意得
设


求导得
①当

②当


③当
则存在

综上得
知识点
台风中,C,A地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区。城市B在A的正东40千米处,B城市处于危险区内的时间为
正确答案
解析
如图,以A为坐标原点,建立平面直角坐标系,则B(40,0),台风中心移动的轨迹为射线y=x(x≥0),而点B到射线y=x的距离
故
知识点
12.已知某运动物体的位移



正确答案
3e
解析
略。
知识点
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
(1)从这60名男生中按是否看营养说明采取分层抽样的方法,抽取一个容量为6的样本,文样本中看与不看营养说明的男生各有多少名?
(2)从(1)中的6名男生样本中随机选取2名作深度采访,求选到看与不看营养说明的男生各1名的概率;
(3)根据以上列联表,是否有
参考公式:

参考值表:
正确答案
见解析。
解析
(1)根据分层抽样可得:样本中看营养说明的男生有
不看营养说明的男生有
(2)记样本中看营养说明的4名男生为
















其中符合要求的是







故所求的概率为
(3)假设

由题设条件得:
因为由

知识点
21.对定义域分别是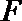
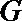
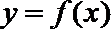
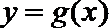
函数
已知函数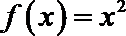
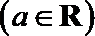
(1)求函数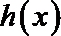
(2)对于实数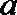
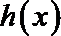
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析