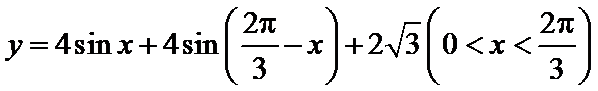- 函数解析式的求解及常用方法
- 共158题
17.在

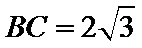
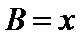

(1)求函数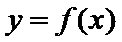
(2)求
正确答案
(1)
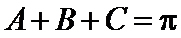
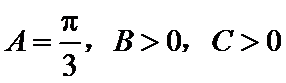
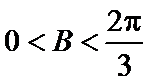
应用正弦定理,知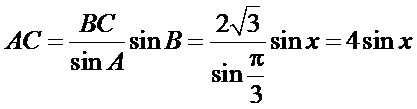

因为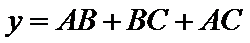
所以
(2)因为

所以,当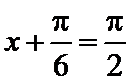
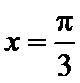
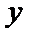
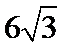
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数



(1)求函数
(2)若数列



(3)在(2)的条件下,证明:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 某上市股票在30天内每股的交易价格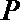

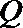
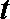
(1)根据提供的图象,写出该种股票每股交易价格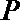
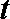
(2)根据表中数据确定日交易量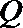

(3)在(2)的结论下,用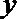
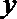
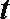
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知:函数



(1)求:
(2)求:
正确答案
(Ⅰ)由题意得
因此
因为函数

即对任意实数x,有
从而3a+1=0,b=0,解得
因此

(Ⅱ)由(Ⅰ)知

令


当


从而


当



由前面讨论知,

而


因此


解析
解析已在路上飞奔,马上就到!
知识点
21.已知平面向量a=(

(1)证明a⊥b;
(2)若存在不同时为零的实数k和t,使x=a+ (t2–3)b,y=–ka+tb,且x⊥y,试求函数关系式k=f(t);
(3)据(2)的结论,讨论关于t的方程f(t)–k=0的解的情况。
正确答案
(1)证明:∵a·b=
(2)解:∵x⊥y,∴x·y=0
即[a+(t2–3)b]·(–ka+tb)=0,整理后得
–ka2+[t–k(t2–3)]a·b+t(t2–3)·b2=0
∵a·b=0,a2=4,b2=1
∴上式化为–4k+t(t2–3)=0,∴k=
(3)解:讨论方程

于是f′(t)=

令f′(t)=0,解得t1=–1,t2=1.当t变化时,f′(t),f(t)的变化情况如下表:
当t=–1时,f(t)有极大值,f(t)极大值=
当t=1时,f(t)有极小值,f(t)极小值=–
而f(t)=


所以f(t)的图象大致如下:
于是当k>

当k=



解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析