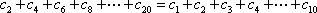- 函数解析式的求解及常用方法
- 共158题
已知向量
(1)求
(2)求函数
正确答案
见解析。
解析
(1)
它的最小正周期为
(2)∵

∴当



当


∴函数

知识点
设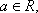
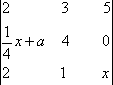
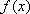

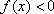
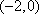
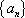

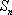
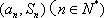
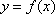
(1)求函数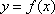
(2)若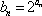
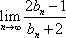
(3)令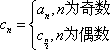
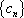
正确答案
见解析
解析
(1)由条件可知,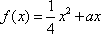
因为关于
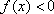
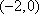
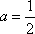
即函数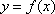
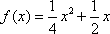
(2)因为点列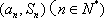
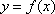
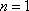
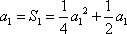
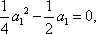
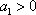
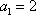
当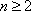
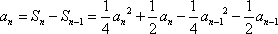
化简得: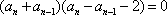
因为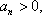
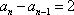
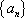
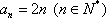
则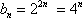
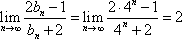
(3)
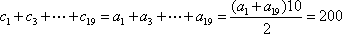

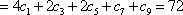
所以,数列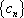
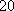
知识点
已知函数

(1)求函数





(2)讨论函数
正确答案
见解析。
解析
(1)




作




所以






(2)









若


若




若



















知识点
某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元。
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该


正确答案
(1)

(2)生产

解析
解析:(1)
由基本不等式得
当且仅当

∴

(2)设总利润为

当

答:生产

知识点
某产品生产成本






(1)产量
(2)产量
正确答案
见解析。
解析
(1)销售收入
利润




(2)每件产品的平均利润













知识点
扫码查看完整答案与解析