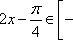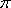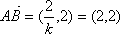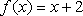- 函数解析式的求解及常用方法
- 共158题
某市地铁连同站台等附属设施全部建成后,平均每1公里需投资人民币1亿元.全部投资都从银行贷款.从投入营运那一年开始,地铁公司每年需归还银行相同数额的贷款本金0.05亿元.这笔贷款本金先用地铁营运收入支付,不足部分由市政府从公用经费中补足. 地铁投入营运后,平均每公里年营运收入(扣除日常管理费等支出后)第一年为0.0124亿元,以后每年增长20%,到第20年后不再增长。
(1)地铁营运几年,当年营运收入开始超过当年归还银行贷款本金?
(2)截至当年营运收入超过当年归还银行贷款本金的那一年,市政府已累计为1公里地铁支付多少元费用?(精确到元,1亿=
正确答案
见解析
解析
(1)地铁营运第


根据题意有:
解得
(或者

答:地铁营运9年,当年营运收入开始超过当年归还银行贷款本金. ……6分
(2)市政府各年为1公里地铁支付费用
第1年:
第2年:
。。。。。。
第



将

答:截至当年营运收入超过当年归还银行贷款本金的那一年,市政府累计为1公里地铁共支付19541135元费用. ………………………………14分
知识点
已知向量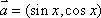
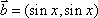
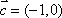
(1)若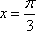
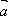
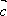
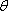
(2)若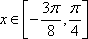
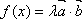

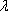
正确答案
见解析
解析
(1)当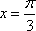
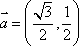
所以 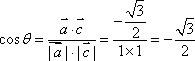
因而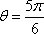
(2)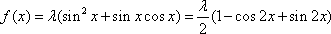

因为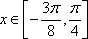
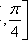
当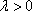
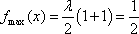
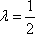
当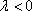
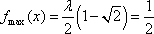
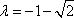
所以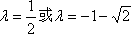
知识点
已知二次函数




(1)求函数
(2)求函数
正确答案
见解析。
解析
(1)








故函数
(2) 


··
当

又
故函数
知识点
已知函数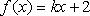
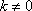

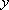
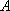
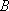
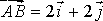
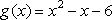

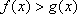
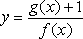
正确答案
-3
解析
由题意知: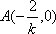
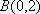
可解得: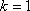
因为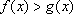
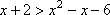
因为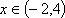
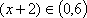
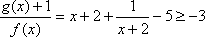
当且仅当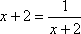
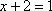
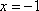
所以,当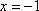
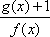
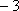
知识点
定义:对函数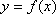
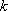
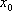
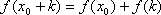
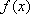
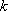
(1)若函数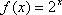
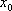
(2)判断函数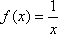
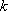
(3)若函数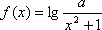

正确答案
见解析
解析
(1)由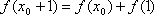
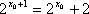
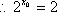
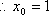
(2)若存在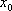

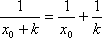
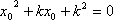
……………………………. 7分
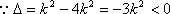

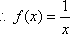
“k性质函数”。 ……………………………. 10分
(3)由条件
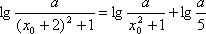
即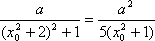
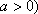
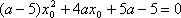
当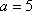
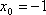
当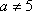

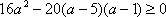
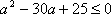
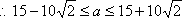
综上,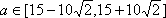
知识点
扫码查看完整答案与解析