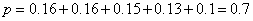- 函数解析式的求解及常用方法
- 共158题
曲线
正确答案
解析
∵

知识点
函数
正确答案

解析
根据二次根式和对数函数有意义的条件,得

知识点
设函数

(1) 当

(2)当




正确答案
见解析
解析
(1)当



(2)当


(i)当




从而当


当


(ii)当

解得:

(注:可用韦达定理判断






综上所述,当


解法2(2)当


故
故

所以 
(1) 解法3:因为

① 当




② 当










作
则

因为


因为

所以
综上所述,所以

知识点
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售。如果当天卖不完,剩下的玫瑰花做垃圾处理。
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式。
(2)花店记录了100天
(i)假设花店在这100天内每天购进17枝玫瑰花,求这100天
(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率。
正确答案
(1)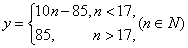
解析
(1)当日需求量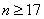
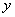
当日需求量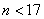
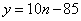
∴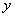
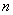
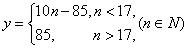
(2)(i)这100天中有10天的日利润为55元,20天的日利润为65元,16天的日利润为75元,54天的日利润为85元,所以这100天的平均利润为
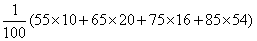
(ii)利润不低于75元当且仅当日需求不少于16枝,故当天的利润不少于75元的概率为
知识点
设集合



①




(1)求
(2)求

正确答案
(1)4;(2)
解析
(1)当


∴ 
( 2 )任取偶数






由条件知,若



于是



设



当



∴
知识点
扫码查看完整答案与解析