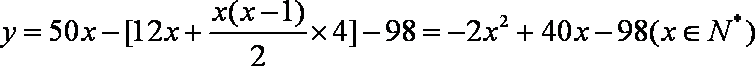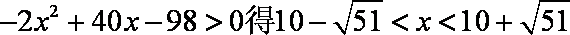- 函数解析式的求解及常用方法
- 共158题
学校要建一个面积为


正确答案
见解析。
解析
设游泳池的长为


依题意,得
………8分
当且仅当

答:游泳池的长为

………10分
知识点
某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/平方米,水池所有墙的厚度忽略不计。
试设计污水处理池的长和宽,使总造价最低,并求出最低总造价
正确答案
见解析。
解析
设污水处理池的宽为x米,则长

则总造价
当且仅当

知识点
机床厂2001初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元。
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值);
(3)使用若干年后,对机床的处理方案有两种:
(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;
(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床。
请你研究一下哪种方案处理较为合理?请说明理由
正确答案
见解析。
解析
(1)依题得:
(2)解不等式
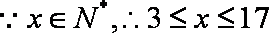
(3)(Ⅰ)
当且仅当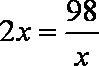
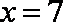

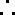
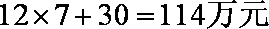
(Ⅱ)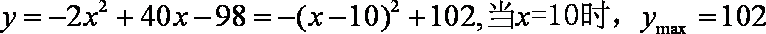
故到2011年,盈利额达到最大值,工厂获利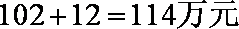
盈利额达到的最大值相同,而方案Ⅰ所用的时间较短,故方案Ⅰ比较合理。
知识点
某企业去年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降,若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+
(1)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为



(2)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
正确答案
见解析。
解析
(1)依题意知,数列


=
=
=
(2)依题意得,

可化简得


又



又
则
知识点
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1)设AD=x(x
注明函数的定义域;
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请给予证明。
正确答案
见解析。
解析
(1)在△ADE中,由余弦定理得:

又
把代入得
∴


即函数的定义域为
(2)如果DE是水管,则
当且仅当


如果DE是参观线路,记
∴函数


故
∴
即DE为AB中线或AC中线时,DE最长.…………………………………………… 12分
知识点
扫码查看完整答案与解析