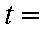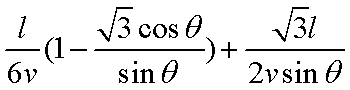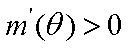- 函数解析式的求解及常用方法
- 共158题
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为t元(t为常数,且


(1)求该工厂的每日利润y元与每公斤蘑菇的出厂价
(2)若t=5,当每公斤蘑菇的出厂价x为多少元时,该工厂的利润y最大,并求最大值。
正确答案
见解析。
解析
(1)设日销量




(2)当





当每公斤蘑菇的出厂价为26元时,该工厂的利润最大,最大值为
知识点
为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为xm时,所砌砖墙的总长度为ym,且在计算时,不计砖墙的厚度,求
(1)y关于x的函数解析式y=f(x);
(2)若BC的长不得超过40m,则当BC为何值时,y有最小值,并求出这个最小值。
正确答案
见解析。
解析
(1)
(2)令
因为

所以
故当x=40m时.y取理最小值225m.
知识点
2010年世博会在上海召开,某商场预计2010年从1月起前x个月顾客对某种世博商品的需求总量P(x)件与月份x的近似关系是:
(1)写出第x月的需求量
(2)若第x月的销售量



正确答案
见解析。
解析
(1)当

当

∴
(2)

∵当



∴ 当


∵当



∴当


综上,预计第6个月的月利润达到最大,最大月利润为3000元
知识点
某运输装置如图所示,其中钢结构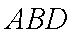
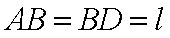
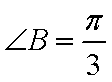
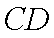
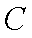
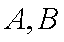
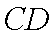
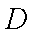
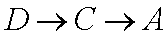
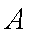
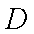
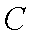
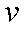
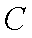
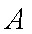
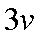
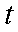
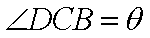
(1)当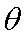
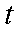
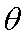
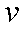
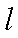
(2)当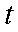
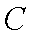
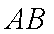
正确答案
见解析。
解析
(1)在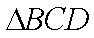
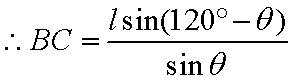
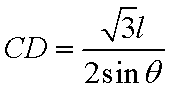
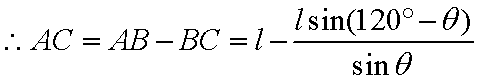
则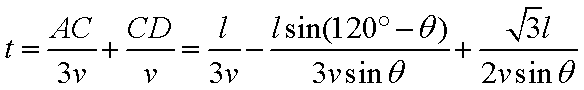
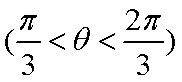
(2)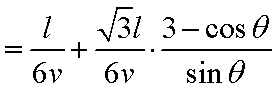
令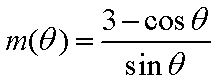
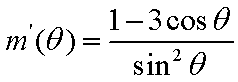
令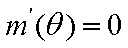
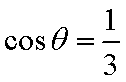
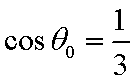
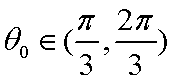
则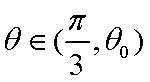
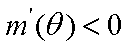
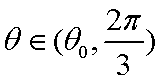
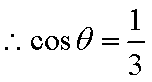
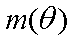
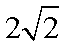
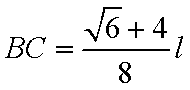
答:当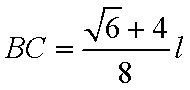
知识点
设函数





(1)求使满足对任意实数




(2)设函数







(注:若函数



(3)是否存在正整数






正确答案
见解析。
解析
(1)







(2)





(3)

①当
而当














综上所述,


②当


当

当










在




综上①②所述:存在

知识点
扫码查看完整答案与解析