函数解析式的求解及常用方法
共158题

· 函数解析式的求解及常用方法

函数解析式的求解及常用方法
共158题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

已知函数（其中的图象与轴

的交点中，相邻两个交点之间的距离为，且图象上一个最低点为。

（1）求的解析式；

（2）当时，求的最大值及相应的的值。

正确答案

见解析。

解析

（1）由题意得，周期，得，此时，

将代入上式得，即，，

解得，所以＝；

（2）因为，所以，

所以，当且仅当，即时，，

即有的最大值为2。

知识点

函数解析式的求解及常用方法

题型：简答题

简答题 · 14 分

某人年底花万元买了一套住房，其中首付万元，万元采用商业贷款，贷款的月利率为‰，按复利计算，每月等额还贷一次，年还清，并从贷款后的次月开始还贷。

（1）这个人每月应还贷多少元？

（2）为了抑制高房价，国家出台“国五条”，要求卖房时按照差额的20%缴税，如果这个人现在将住房万元卖出，并且差额税由卖房人承担，问：卖房人将获利约多少元？（参考数据：）

正确答案

见解析

解析

（1）设每月应还贷元，共付款次，则有

所以（元）

答：每月应还贷元

（2）卖房人共付给银行元，

利息（元）

缴纳差额税（元）

（元）。

答：卖房人将获利约元

知识点

函数解析式的求解及常用方法

题型：简答题

简答题 · 12 分

已知函数是定义在实数集R上的奇函数，当＞0时，

（1）已知函数的解析式；

（2）若函数在区间上是单调减函数，求a的取值范围；

（3）试证明对.

正确答案

见解析。

解析

（1） …………1分

时， …………3分

所以 …………4分

（2）函数是奇函数，则在区间上单调递减，当且仅当在区间上单调递减，当时， …………6分

由＜0得＜在区间（1，+）的取值范围为……（8分）

所以a的取值范围为…………………………………………………………（9分）

（3）……（10分）解得（11分），因为1＜e—1＜e，所以为所求………………………………………（12分）

知识点

函数解析式的求解及常用方法函数单调性的性质函数奇偶性的性质利用导数研究函数的单调性

题型：单选题

单选题 · 5 分

已知函数是偶函数，且，当时，，=则方程在区间上的解的个数是（）

C10

D11

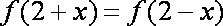
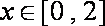
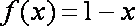
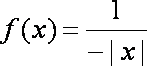
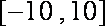
正确答案

解析

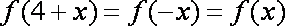
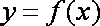
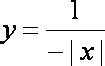
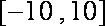
由题意可得，函数的周期是4，可将问题转化为与在区间有几个交点。画图知，有10个交点,选C。

知识点

函数解析式的求解及常用方法

题型：简答题

简答题 · 15 分

请你为某养路处设计一个用于储藏食盐的仓库（供融化高速公路上的积雪之

用），它的上部是底面圆半径为5m的圆锥，下部是底面圆半径为5m的圆柱，且该仓库的总高度

为5m，经过预算，制造该仓库的圆锥侧面、圆柱侧面用料的单价分别为400元/、100元/，

问当圆锥的高度为多少时，该仓库的侧面总造价（单位：元）最少？

正确答案

见解析。

解析

（法一）设圆锥母线与底面所成角为，且，

则该仓库的侧面总造价

，

由得，即，

经检验得，当时，侧面总造价最小，此时圆锥的高度为m。

（法二）设圆锥的高为m，且，

则该仓库的侧面总造价

，

由得，

经检验得，当时，侧面总造价最小，此时圆锥的高度为m。

知识点

函数解析式的求解及常用方法

继续学习学习下一知识点

下一知识点 : 区间与无穷的概念

百度题库 > 高考 > 文科数学 > 函数解析式的求解及常用方法

扫码查看完整答案与解析