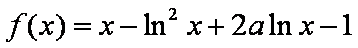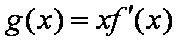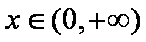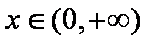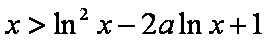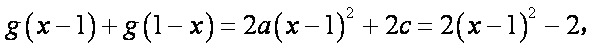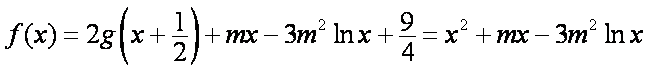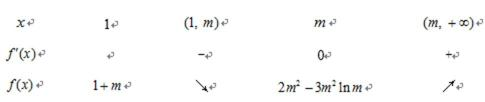- 函数解析式的求解及常用方法
- 共158题
设常数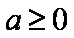
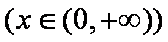
(1)令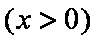
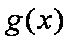
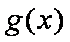
(2)求证: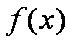
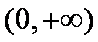
(3)求证:当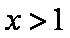
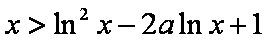
正确答案
见解析。
解析
(1)∵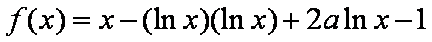
∴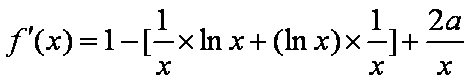
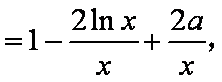
∴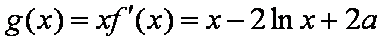
∴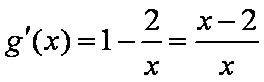
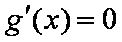
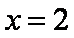
列表如下:
∴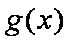
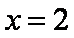
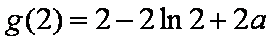
即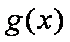
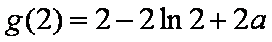
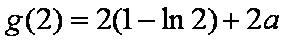
∵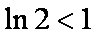
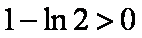
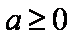
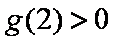
证明(2)由(1)知,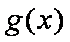
∴对一切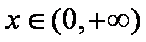
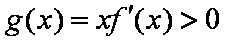
从而当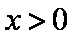
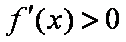
故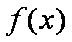
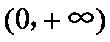
证明(3)由(2)知: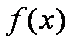
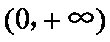
∴当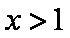
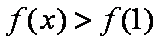
又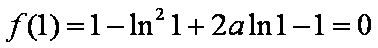
∴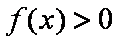
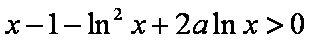
∴
故当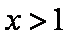
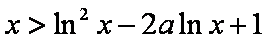
知识点
某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率



(注:次品率=次品数/生产量,如
已知每生产1万件合格的仪器可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量。
(1)试将生产这种仪器的元件每天的盈利额

(2)当日产量为多少时,可获得最大利润?
正确答案
见解析
解析
(1)当

当

综上,日盈利额


(2)由(1)知,当
当
当且仅当
所以(i)当

(ii)当

函数


综上,若
若

知识点
某化工企业2007年底投入100万元,购入一套污水处理设备,该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元。
(1)求该企业使用该设备

(2)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
正确答案
见解析。
解析
(1)
即

(将定义域写成
由均值不等式得:
(2)
当且仅当

答:该企业10年后需要重新更换新设备。
知识点
为配合国庆黄金周,促进旅游经济的发展,某火车站在调查中发现:开始售票前,已有a人在排队等候购票,开始售票后,排队的人数平均每分钟增b人,假设每个窗口的售票速度为c人/分钟,且当开放两个窗口时,25分钟后恰好不会出现排队现象(即排队的人刚好购完);若同时开放三个窗口时,则15分钟后恰好不会出现排队现象。
(1)若要求售票10分钟后不会出现排队现象,则至少需要同时开几个窗口?
(2)若a=60,在只开一个窗口的情况下,试求第n(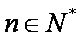
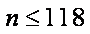
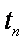
(注:购票者的等待时间指从开即始排队(售票开始前到达的人,从售票开始计时)到开始购票时止)
正确答案
见解析。
解析
(1)设需同时开x个窗口,
则根据题意有,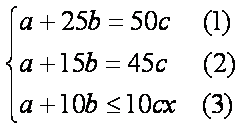
由(1)(2)得,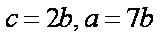
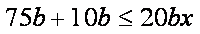
∴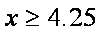
(2)由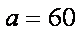
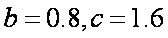
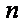
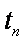
当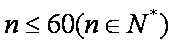
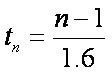
当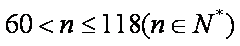
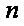
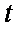
则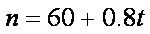
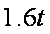
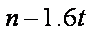
∴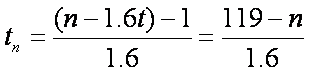
综上,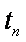
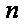
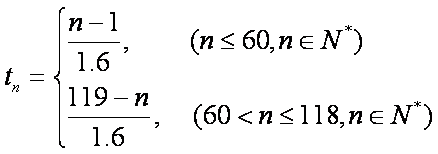
∵当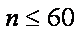
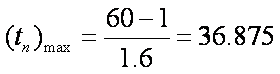
当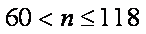
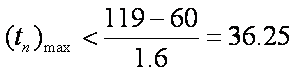
∴第60个购票者的等待时间最长。
知识点
已知二次函数g(x)对任意实数x都满足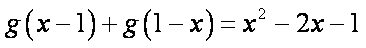
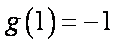
令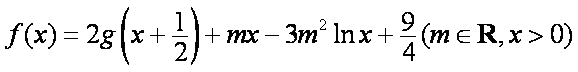
(1)求 g(x)的表达式;
(2)若函数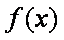
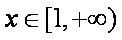
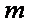
(3)记函数

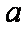
正确答案
见解析。
解析
(1)设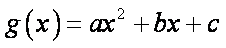
所以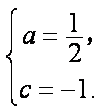
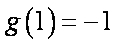
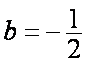
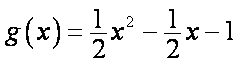
(2)
则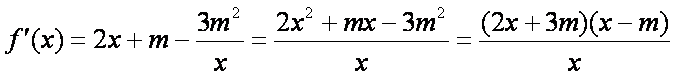
令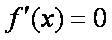
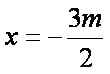
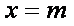
①当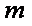
∴当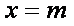
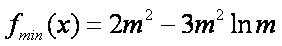
令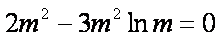
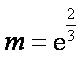
②当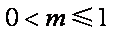
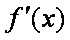
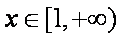
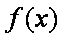
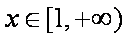
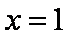
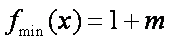
令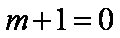
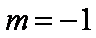
综上所述,所求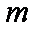
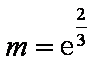
(3)记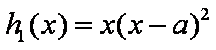
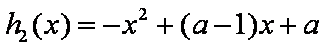
则据题意有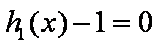
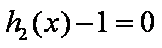
且这5个实根两两不相等。
(ⅰ)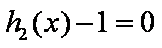
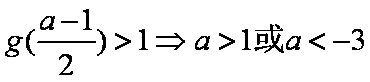
(ⅱ)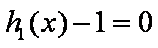
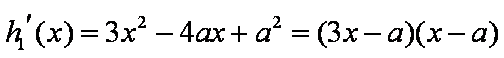
令
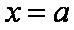
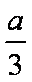
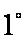
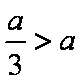
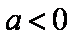
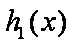
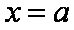
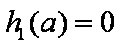
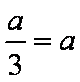
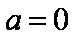
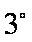
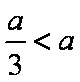
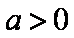
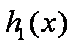
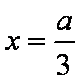
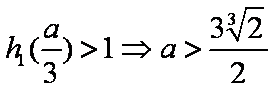
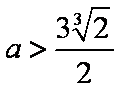
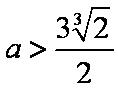
下证:这5个实根两两不相等,
即证:不存在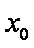
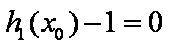
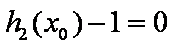
若存在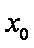
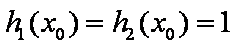
由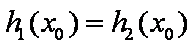
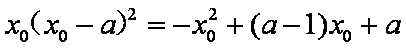
得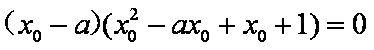
当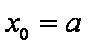
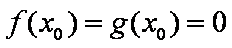
当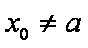
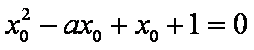
又由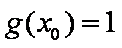
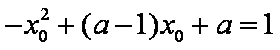
联立①②式,可得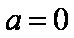
而当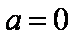
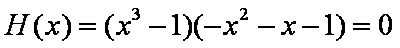
所以这5个实根两两不相等。
综上,当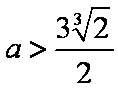
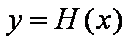
知识点
扫码查看完整答案与解析