- 函数解析式的求解及常用方法
- 共158题
武汉地区春天的温度的变化曲线近似地满足函数

(1)写出这段曲线的函数解析式;
(2)求出一天(

正确答案
见解析
解析
解析:(1)由条件可知

因为


将点


(2)由(1),令
得
所以
或
由①,得


由②,得




即一天温度的变化在



知识点
已知函数f(x)=


正确答案

解析
法1 注意到函数

由

所以


结合函数是偶函数得原问题中

法2 
作出函数

并注意到


知识点
某一电视频道在一天内有x次插播广告的时段,一共播放了y条广告,第1次播放了1条和余下的y-1条的,第2次播放了2条以及余下的,第3次播放了3条以及余下的,以后每次按此规律插播广告,在第x次播放了余下的x条(x>1)。
(1)设第k次播放后余下ak条,这里a0=y,ax=0,求ak与ak-1的递推关系式;
(2)求这家电视台这一天内播放广告的时段x与广告的条数y.
正确答案
见解析
解析
(1)依题意,第k次播放了k+(ak-1-k)=ak-1+k,∴ak=ak-1-(ak-1+k)。
∴ak-1=k+ak,即ak与ak-1的递推关系式为ak-1=k+ak.
(2)∵a0=1+a1=1+(2+a2)=1+2×+()2a2
=1+2×+3×()2+()3a3=…
=1+2×+3×()2+…+x×()x-1+()xax.
∵ax=0,∴y=1+2×+3×()2+…+x×()x-1.
用错位相减法求和,可得y=49+(x-7)×.
故这家电视台这一天播放广告的时段为7段,广告的条数为49.
知识点
函数y=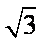
正确答案
π
解析
y=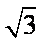
知识点
函数y=lg
正确答案
(lg2,+∞)
解析
解:由题设知10x﹣2>0,
解得x>lg2。
∴函数y=lg
知识点
由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项.按图中多边形的边数依次称这些数列为“三角形数列”、“四边形数列”




(1)求使得

(2)试推导


正确答案
见解析
解析
解析:(1)
由题意得
所以,最小的
(2)设


从图中可以得出:后一层的点在
所以

所以

所以

知识点
如图1,



















(1)求
(2)试写出三角形观光平台


正确答案
见解析。
解析
(1)由题意,得


又因为过点M要分别修建与OA、OB平行的栈桥MG、MK,
所以
所以

(2)由题意,得
所以
则
因为函数

所以当
知识点
函数

(1)求函数
(2)设


正确答案
见解析
解析
(1)∵函数
∴ 
∵函数图象的相邻对称中心之间的距离为
∴
故函数
(2)∵
∴
则 

即所求
知识点
已知函数


(1)求函数
(2)若对于区间



(3)若过点


正确答案
(1)
解析
解析:(1)
根据题意,得
解得

(2)令



则对于区间[-2,2]上任意两个自变量的值
所以

(3)设切点为


则
即
因为过点

所以方程
即函数
则
令
…………10分



知识点
如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天
花板上,圆环呈水平状态,并且与天花板的距离
环上设置三个等分点A1,A2,A3。点C为
同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3
的长度相等。设细绳的总长为
(1)设∠CA1O = 
(2)请你设计
指明此时 BC应为多长。
正确答案
见解析。
解析
(1)解:在





(2)
令

当



∵

∴当角



知识点
扫码查看完整答案与解析




































