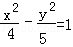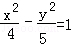- 双曲线及其性质
- 共445题
已知F1、F2分别为双曲线C:
正确答案
6
解析
知识点
已知双曲线




(1)求

(2)记直线




正确答案
见解析。
解析
(1)


由




由于





(2)由已知可得



由①,得

知识点
曲线

正确答案
解析
略
知识点
若双曲线


正确答案
解析
略
知识点
已知中心在原点,焦点在x轴上的双曲线的离心率为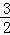
正确答案
解析
∵ 双曲线中心在原点,焦点在x轴上
∴ 设双曲线方程为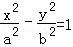
∵ 双曲线的离心率为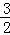
∴ 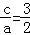
由此可得b2=c2﹣a2=5
∴ 双曲线的方程是
知识点
若双曲线







正确答案
解析
双曲线焦点到渐近线的距离为


















知识点
设双曲线


正确答案
解析
略
知识点
双曲线








正确答案
解析
略
知识点
若双曲线






正确答案
解析
双曲线焦点到渐近线的距离为













知识点
已知双曲线


正确答案
解析
双曲线的左顶点为















知识点
扫码查看完整答案与解析