双曲线及其性质
共445题

双曲线及其性质
共445题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

由曲线y=x2，y=x3围成的封闭图形面积为　　。

正确答案

解析

要求曲线y=x2，y=x3围成的封闭图形面积，根据定积分的几何意义，只要求∫01（x2﹣x3）dx即可。

解：由题意得：所求封闭图形的面积为

∫01（x2﹣x3）dx═（﹣）|01

=，

故答案为：。

知识点

双曲线的几何性质

题型：填空题

填空题 · 5 分

若抛物线y2=2px（p＞0）的焦点与双曲线的右焦点重复，则p=　　。

正确答案

解析

双曲线中a2=12，b2=4，∴c2=a2+b2=14，∴c=4

∴双曲线的右焦点为（4，0）

∵抛物线y2=2px（p＞0）的焦点与双曲线的右焦点重复，

∴

∴p=8

故答案为：8

知识点

双曲线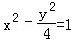的几何性质抛物线的标准方程和几何性质

题型：单选题

单选题 · 5 分

双曲线的渐近线方程为（　　）

Ax=±1

By=±2

Cy=±2x

Dx=±2y

正确答案

解析

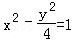
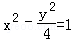
在双曲线的标准方程中，把等号右边的1换成0，即得双曲线的渐近线方程

y=±2x，

故选 C。

知识点

双曲线的几何性质

题型：单选题

单选题 · 5 分

设和为双曲线()的两个焦点，若，是正三角形的三个顶点，则双曲线的离心率为（）

正确答案

解析

由有，则，故选B

知识点

双曲线的几何性质

题型：填空题

填空题 · 5 分

已知双曲线上一点M到两个焦点的距离分别为20和4，则该双曲线的离心率为______。

正确答案

解析

略

知识点

双曲线的定义及标准方程双曲线的几何性质

题型：填空题

填空题 · 4 分

已知抛物线的准线过双曲线的右焦点，则双曲线的离心率为 .

正确答案

解析

略

知识点

双曲线的几何性质抛物线的标准方程和几何性质

题型：填空题

填空题 · 4 分

已知双曲线的右焦点为(，0)，则该双曲线的渐近线方程为 ·

正确答案

解析

略

知识点

双曲线的几何性质

题型：填空题

填空题 · 4 分

设双曲线的离心率为2，且一个焦点与抛物线的焦点相同，则此双曲线的方程为 ▲ .

正确答案

解析

略

知识点

双曲线的几何性质

题型：单选题

单选题 · 5 分

以双曲线的焦点为顶点，顶点为焦点的椭圆的离心率为，

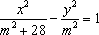
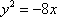
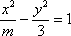
正确答案

解析

易知椭圆中，故选A。

知识点

椭圆的几何性质双曲线的几何性质

题型：简答题

简答题 · 16 分

已知点为双曲线的左、右焦点，过作垂直于轴的直线，在轴上方交双曲线于点，且，圆的方程为.

（1）求双曲线的方程；

（2）若双曲线上的点到两条渐近线的距离分别为，求的值；

（3）过圆上任意一点作切线交双曲线于两个不同点，求的值.

正确答案

见解析

解析

（1）设的坐标分别为-------------------1分

因为点在双曲线上，所以，即，所以------------2分

在中，，，所以------------3分

由双曲线的定义可知：

故双曲线的方程为：-------------------4分

（2）由条件可知：两条渐近线分别为-------------------5分

设双曲线上的点，

则点到两条渐近线的距离分别为-------------------7分

所以-------------------8分

因为在双曲线：上，所以-------------------9分

故-------------------10分

（3）解一：因为为圆：上任意一点，设

所以切线的方程为：-------------------12分

代入双曲线：

两边除以，得-------------------13分

设，则是上述方程的两个根

由韦达定理知：，即-------------------15分

所以-------------------16分

解二：设，切线的方程为：-------------------12分

①当时，切线的方程代入双曲线中，化简得：

所以：-------------------13分

又

所以-----------15分

②当时，易知上述结论也成立。

所以-------------------16分

知识点

双曲线的几何性质

继续学习学习下一知识点

下一知识点 : 抛物线及其性质

百度题库 > 高考 > 文科数学 > 双曲线及其性质

扫码查看完整答案与解析