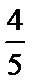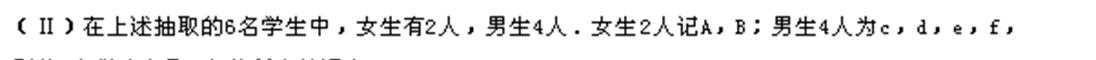- 简单随机抽样
- 共28题
4.某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。图中A点表示十月的平均最高气温约为15°C,B点表示四月的平均最低气温约为5°C。下面叙述不正确的是
正确答案
考查方向
解题思路
根据图中的最高气温和最低气温线观察分析。
易错点
审题要清晰,答案要求找不正确的;再者读图要细致,根据选择支语句加强讨论。
知识点
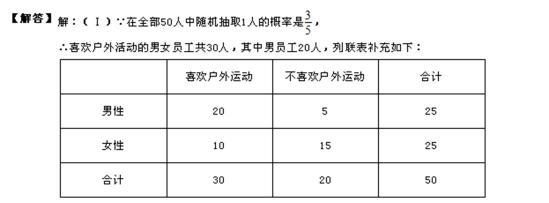
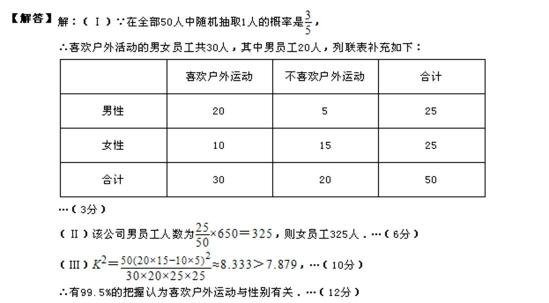
为了提高全民的身体素质,某地区增加了许多的户外运动设施为本地户外运动提供服务,为了进一步了解人们对户外运动的喜爱与否,随机对50人进行了问卷调查,已知在这50人中随机抽取1人抽到喜欢户外运动的概率为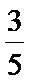
19.请将上面的列联表补充完整;
20.是否有99.5%的把握认为“喜欢户外运动与性别有关”?并说明你的理由;
21.根据分层抽样的方法从喜欢户外运动的人中抽取6人作为样本,从6人中随机抽取三人进行跟踪调查,那么这三人中至少有一名女性的概率是多少?
下面的临界值表仅供参考:
(参考公式: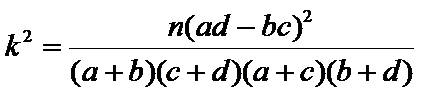
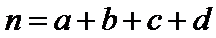
正确答案
见解析
解析
考查方向
解题思路
易错点
分层时候计算问题。再就是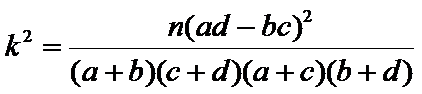
正确答案
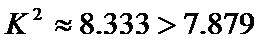
解析
考查方向
解题思路
易错点
分层时候计算问题。再就是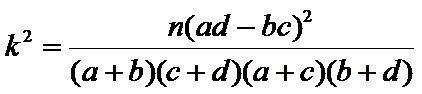
正确答案
解析
从六人中选出三人的方法数为n=20.其中三人中至少有一名女性的事件与没有女生的事件是对立事件,没有女生的基本事件数为4,所以概率为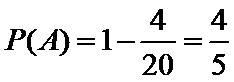
考查方向
解题思路
易错点
分层时候计算问题。再就是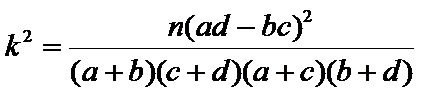
某工厂36名工人的年龄数据如下表。
工人编号 年龄
工人编号 年龄
工人编号 年龄
工人编号 年龄
1 40
2 44
3 40
4 41
5 33
6 40
7 45
8 42
9 43
10 36
11 31
12 38
13 39
14 43
15 45
16 39
17 38
18 36
19 27
20 43
21 41
22 37
23 34
24 42
25 37
26 44
27 42
28 34
29 39
30 43
31 38
32 42
33 53
34 37
35 49
36 39
18.用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
19.计算(1)中样本的平均值

20.36名工人中年龄在

正确答案
(1)








解析

考查方向
解题思路
第一问,利用系统抽样抽取样本,知道第一组中抽取的编号,依次加上组距4,即可抽出所有样本数据。
易错点
系统抽样的选取办法,均值方差的计算。
正确答案


解析



方差为


考查方向
解题思路
第二问,直接利用均值和方差的公式计算即可。
易错点
系统抽样的选取办法,均值方差的计算。
正确答案
(3)

解析








考查方向
解题思路
第三问,利用第二问,得出均值和标准差之后,找到所在区域中的数据个数,然后估算出所占比例即可。
易错点
系统抽样的选取办法,均值方差的计算。
某班同学
年龄段分组
[20,25)
[25,30)
[30,35)
[35,
[40,45)
频数
300
320
160
160
40
20
19.在答题卡上作出这些数据的频率分布直方图;
20.估计年龄段的“低头族”的平均年龄(同一组中的数据用该组区间的中点值作代表);
21.从年龄段在[25,35)的“低头族”中采用分层抽样法抽取6人接受采访,并从6人中随机选取2人作为嘉宾代表,求选取的2名嘉宾代表中恰有1人年龄在[25,30)岁的概率.
正确答案
略
正确答案
设“低头族”平均年龄为
则

正确答案
略
8.某学校共有老、中、青职工200人,其中有老年职工60人,中年职工人数与青年职工人数相等.现采用分层抽样的方法抽取部分职工进行调查,已知抽取的老年职工有12人,则抽取的青年职工应有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
某产品按行业生产标准分成







(1)从该厂生产的产品中随机抽取
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
该行业规定产品的等级系数


(2)已知该厂生产一件该产品的利润y(单位:元)与产品的等级系数



正确答案
见解析
解析
解析:(1)由样本数据知,30件产品中等级系数
∴样本中一等品的频率为

二等品的频率为

三等品的频率为

(2)∵
用样本的频率分布估计总体分布,将频率视为概率,由(1)可得


∴可得
其数学期望
知识点
为调查某校学生喜欢数学课的人数比例,采用如下调查方法:
(1)在该校中随机抽取100名学生,并编号为1,2,3, ,100;
(2)在箱内放置两个白球和三个红球,让抽取的100名学生分别从箱中随机摸出一球,记住其颜色并放回;
(3)请下列两类学生举手:(ⅰ)摸到白球且号数为偶数的学生;(ⅱ)摸到红球且不喜欢数学课的学生.
如果总共有26名学生举手,那么用概率与统计的知识估计,该校学生中喜欢数学课的人数比例大约是( )
正确答案
解析
设该校学生中喜欢数学课的人数比例大约是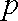
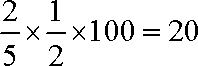

知识点
16.(本小题满分13分)某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从三个社团成员中抽取18人,结果拳击社被抽出了6人.
(1)求拳击社团被抽出的6人中有5人是男生的概率;
(2)设拳击社团有X名女生被抽出,求X的分布列.
正确答案
见解析。
解析
(1)由于按分层抽样的方法从三个社团成员中抽取18人,拳击社被抽出了6人,
∴
∴m=2.
设A为“拳击社团被抽出的6人中有5人是男生”,
则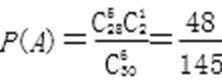
(2)由题意可知:X=0,1,2,

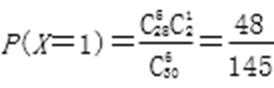

X的分布列为
知识点
扫码查看完整答案与解析