热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

12．已知A、B、C为△ABC的三个内角，向量m满足｜m｜＝，且m＝（，），若A最大时，动点P使得｜｜、｜｜、｜｜成等差数列，则的最大值是

正确答案

解析

如图假设AB=2，BC= 如图建系

∴P的轨迹为椭圆且

考查方向

本题考察了向量的模长的几何意义，考察了圆，椭圆的标准方程，考察了函数求最值

解题思路

1)由向量向量m的模长得出得出A最大值以及B，C的值，确定三角形的形状，

2)动点P使得｜｜、｜｜、｜｜成等差数列得出点P的轨迹是椭圆

3)由｜｜是定值，得出只需求|PA|的最大值即可

4)根据一元二次函数的性质得出结果

易错点

主要易错于几何意义的构建

知识点

三角形中的几何计算数列与三角函数的综合

题型：填空题

填空题 · 12 分

在△ABC中，a、b、c分别是∠A、∠B、∠C的对边长，已知a、b、c成等比数列，且a2－c2＝ac－bc，求∠A的大小及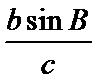的值．

正确答案

∠A＝60°；.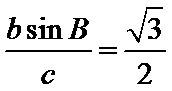

考查方向

本题考查了正余弦定理在解三角形的应用；

易错点

1、对a、b、c成等比结合a2－c2＝ac－bc的化简方向的选择

知识点

三角函数中的恒等变换应用数列与三角函数的综合

题型：填空题

填空题 · 5 分

14．设向量=（cos，sin+cos）（k=0，1，2，…，12），则（ak•ak+1）的值为　　．

正确答案

解析

=++++

=++

=++，

∴（ak•ak+1）=+++++++…+++++++…+

=+0+0

=．

故答案为：9．

考查方向

本题考查了向量数量积运算性质、两角和差的正弦公式、积化和差公式、三角函数的周期性，考查了推理能力与计算能力，属于中档题．

解题思路

利用向量数量积运算性质、两角和差的正弦公式、积化和差公式、三角函数的周期性即可得出．

易错点

本题考查了向量数量积运算性质、两角和差的正弦公式、积化和差公式、三角函数的周期性,在应用公式解题过程中易错.

知识点

数列与三角函数的综合

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 数列与解析几何的综合

百度题库 > 高考 > 理科数学 > 数列与三角函数的综合

扫码查看完整答案与解析