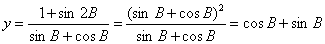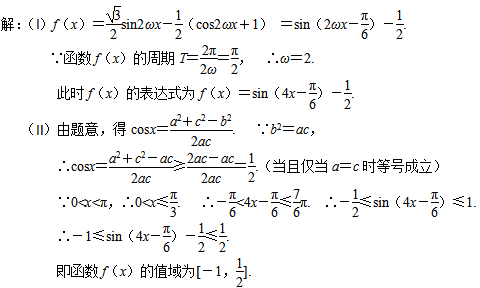- 余弦定理的应用
- 共46题
1
题型:简答题
|
在




(1)求角
(2)设



正确答案
见解析
解析
(1)由

又

由


得
(2)


知识点
余弦定理的应用
1
题型:简答题
|
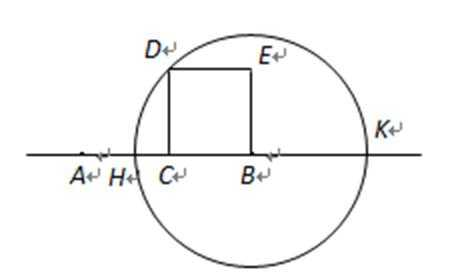
如图,设C为线段AB的中点,BCDE是以BC为一边的正方形,以B为圆心,BD为半径的圆与AB及其延长线相交于点H及K。
(1)求证:HC·CK=BC2;
(2)若圆的半径等于2,求AH·AK的值。
正确答案
见解析
解析
(1)连结DH,DK,则DH⊥DK,
∴△DHC∽△KDC,∴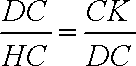
又DC=BC,∴BC2=HC·CK……………………………………………………(5分)
(2)连结AD,则AD⊥BD,AD=BD,∴AD是⊙B的切线,于是AD2=AH·AK,
∴AH·AK=4………………………………………………………………………(10分)
知识点
余弦定理的应用
1
题型:简答题
|
18.已知:△ABC中,角A、B、C所对的三边a,b,c成等比数列。
(1)求证: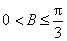
(2)求函数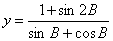
正确答案
解:(1)∵a、b、c成等比数列,
∴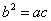
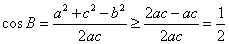
∵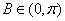
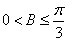
(2)由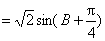
∵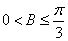
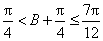
∴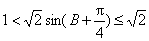
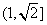
解析
解析已在路上飞奔,马上就到!
知识点
正弦函数的定义域和值域二倍角的正弦余弦定理的应用
1
题型:简答题
|
17.设函数
(1)求


(2)已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
三角函数中的恒等变换应用余弦定理的应用三角函数的最值
1
题型:简答题
|
15.已知函数f(x)=sinωx·cosωx-cos2ωx(ω>0)的最小正周期为.
(Ⅰ)求ω的值;
(Ⅱ)设△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,求此时f(x)的值域.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
余弦定理的应用
下一知识点 : 三角形中的几何计算
扫码查看完整答案与解析