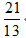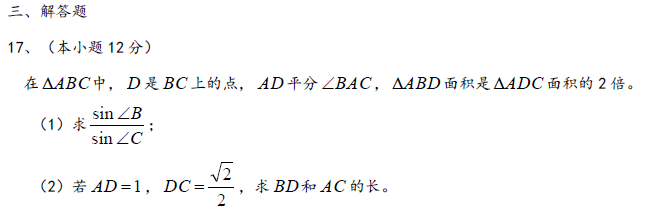余弦定理的应用
共46题

· 余弦定理的应用

余弦定理的应用
共46题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

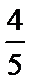
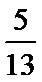
13.△ABC的内角A、B、C的对边分别为a、b、c，若cos A=，cos C=，a=1，则b= .

正确答案

知识点

正弦定理的应用余弦定理的应用

题型：简答题

简答题 · 12 分

19．在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域，点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船位于点A北偏东45º且与点A相距40海里的位置B，经过40分钟又测得该船已行驶到点A北偏东45º+（其中，）且与点A相距海里的位置C.

（1）求该船的行驶速度（单位:海里/小时）

（2）若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理的应用余弦定理的应用解三角形的实际应用

题型：填空题

填空题 · 4 分

12．如图为了测量，两点间的距离，选取同一平面上，两点，测出四边形各边的长度（单位：）:AB=5,BC=8,CD=3,DA=5,如图所示，且A．B．C．D四点共圆，则的长为______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

余弦定理的应用

题型：简答题

简答题 · 10 分

17．在△ABC中，内角A、B、C所对边的长分别为a、b、c，已知向量=(1,cosA -1)，=(cosA,1)且满足⊥.

（1）求A的大小；

（2）若a=，b+c=3 求b、c的值。

正确答案

（1），cosA=, A为△ABC内角，∴A=60º

（2）a=,A=60º,由余弦定理a2=b2+c2-2bccosA

得a2=(b+c)2-2bc-2bccosA

∵b+c=3,

∴3=9-3bc,bc=2

由

得

解析

解析已在路上飞奔，马上就到！

知识点

余弦定理的应用

题型：简答题

简答题 · 12 分

17．在中，分别为角的对边，为锐角，已知向量，，且。

（1）若，求实数的值；

（2）若，求面积的最大值，以及面积最大时边的大小。

正确答案

（1）；

（2）当且仅当时成立

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用余弦定理的应用平行向量与共线向量平面向量的坐标运算

题型：单选题

单选题 · 5 分

4．在极坐标中，过点（2，0）并且与极轴垂直的直线方程是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

余弦定理的应用

题型：简答题

简答题 · 12 分

19．（1）求证：sinα·sinβ=[cos(α-β)一cos(α+β)]；

（2）在锐角△ABC中，∠ A=60°，BC=2，求△ABC面积的取值范围．

正确答案

（1）略；

（2）．

解析

本题属于三角函数中的基本问题，题目的难度是逐渐由易到难．

（1）由，，

两式相减得：。

（2）由正弦定理可知，

由，

所以.

考查方向

本题考查了三角函数的积化和差的证明及解三角形的问题．属于高考中的高频考点。

解题思路

无

易错点

注意锐角三角形的条件，忽视则容易出错。

知识点

两角和与差的余弦函数余弦定理的应用

题型：简答题

简答题 · 14 分

20．如图，，，三地有直道相通，千米，千米，千米.现甲、乙两警员同时从地出发匀速前往地，经过小时，他们之间的距离为（单位：千米）.甲的路线是，速度为千米/小时，乙的路线是，速度为千米/小时.乙到达地后原地等待.设时乙到达地.

（1）求与的值；

（2）已知警员的对讲机的有效通话距离是千米.当时，求的表达式，并判断在上得最大值是否超过？说明理由.

正确答案

（1），

（2），不超过.

解析

（2）甲到达用时小时；乙到达用时小时，从到总用时小时．

当时，

；

当时，.

所以.

因为在上的最大值是，在上的最大值是，所以在上的最大值是，不超过.

知识点

分段函数的解析式求法及其图象的作法余弦定理的应用

题型：简答题

简答题 · 12 分

19. 在△ABC中，角A，B，C的对边分别为a，b，c，且满足(a－c) ＝c

（1）求角B的大小；

（2）若||＝，求△ABC面积的最大值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的化简求值正弦定理的应用余弦定理的应用平面向量数量积的运算向量在几何中的应用

题型：简答题

简答题 · 12 分

正确答案

知识点

正弦定理的应用余弦定理的应用三角形中的几何计算

继续学习学习下一知识点

下一知识点 : 三角形中的几何计算

百度题库 > 高考 > 理科数学 > 余弦定理的应用

扫码查看完整答案与解析