函数的概念与基本初等函数_章节学习

1

题型：简答题

|

简答题 · 10 分

选考题:请在22～24题中,选做其中的一题．

22．如图，已知是⊙O的切线，为切点，是⊙O的割线，与⊙O交于两点，圆心在的内部，点是的中点．

（Ⅰ）证明四点共圆；

（Ⅱ）求的大小．

23．直角坐标系中，直线的参数方程为，（是参数），在以为极点，轴的正半轴为极轴的极坐标系中，曲线的极坐标方程为．

（Ⅰ）求直线的普通方程及曲线的直角坐标方程；

（Ⅱ）若与分别是直线与曲线上的动点，求的最小值．

24．设函数．

（Ⅰ）若，解不等式；

（Ⅱ）如果，求a的取值范围．

正确答案

22.

23.

24.

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：单选题

|

单选题 · 5 分

3.已知关于的方程的两个实数根满足，，则实数的取值范围是（）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：单选题

|

单选题 · 5 分

6.设是等差数列的前项和，若，则（）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：单选题

|

单选题 · 5 分

9. 已知为上的可导函数，当时，，则关于的函数的零点个数为（）

A0

B1

C2

D3

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：单选题

|

单选题 · 5 分

10.在△ABC所在平面上有三点P、Q、R，满足则的面积与的面积之比为（）

A1:2

B

C12:13

D13:25

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：填空题

|

填空题 · 5 分

11.函数的定义域为______.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：填空题

|

填空题 · 5 分

14. 定义在上的函数满足是偶函数且是奇函数，又，则_______；

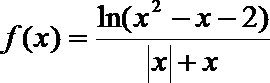
正确答案

-2013

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：简答题

|

简答题 · 12 分

21．已知函数．

（Ⅰ）求函数的单调区间；

（Ⅱ）设，若对任意，，不等式恒成立，求实数的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：单选题

|

单选题 · 5 分

5. 已知函数（其中）的部分图象如右图所示，为了得到的图象，则只需将的图象（）

A向右平移个长度单位

B向右平移个长度单位

C向左平移个长度单位

D向左平移个长度单位

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：单选题

|

单选题 · 5 分

7.若正数满足，则的取值范围是（）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：简答题

|

简答题 · 13 分

19.设数列的前项和为，点在直线上，.

（1）求证：数列是等比数列，并求其通项公式；

（2）设直线与函数的图像交于点，与函数的图像交于点，记（其中为坐标原点），求数列的前项和.

正确答案

解：（1）由题可知：，时.

两式相减，得.

又，.

数列数列是以1为首项，为公比的等比数列.

故.

（2）根据题意得：.

两式相减得：

化简得：

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：单选题

|

单选题 · 5 分

6.直线的倾斜角的变化范围是(　　)

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：简答题

|

简答题 · 12 分

16．在中，内角的对边分别为已知．

（1）求的值；

（2）求的值．

正确答案

解：（1）由题可知：，又，故.

由余弦定理可知

=.即

（2）由（1）知，

则有

.

故=

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：简答题

|

简答题 · 13 分

21.已知函数.

（Ⅰ）若在处取得极大值，求实数a的值；

（Ⅱ）若，直线都不是曲线的切线，求的取值范围；

（Ⅲ）若，求在区间［0，1］上的最大值。

正确答案

解：（Ⅰ）因为

令，所以随的变化情况如下表：

所以

（由得出，或，在有单调性验证也可以（标准略））

（Ⅱ）因为

因为，直线都不是曲线的切线，

所以无实数解

只要的最小值大于

所以

（Ⅲ）因为，所以，

当时，对成立

所以当时，取得最大值

当时，在时，，单调递增

在单调递减

所以当时，取得最大值

当时，在时，，单调递减

所以当，取得最大值

当时，在时，单调递减

在时，，单调递增

又，

当时，在取得最大值

当时，在，处都取得最大值0.

综上所述:

当时，取得最大值

当时，在，处都取得最大值0

当时，在取得最大值.

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

1

题型：填空题

|

填空题 · 5 分

12.已知函数在单调递增，则实数的取值范围为______.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点