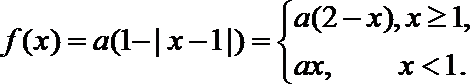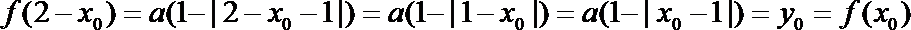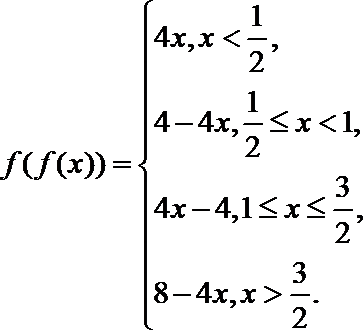- 函数的概念与基本初等函数
- 共5812题
3.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数




正确答案
(1,3)
解析
解析已在路上飞奔,马上就到!
知识点
16.



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数


正确答案


若
则

此时,

又





解析
解析已在路上飞奔,马上就到!
知识点
20.甲.乙两地相距



(1)将全程运输成本

(2)为了使全程运输成本最小,货车应以多大的速度行驶。
正确答案
(1)
(2)







当
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数


(1)设


(2)设计一个函数


(3)








正确答案
(1)

(2)
若

(3)
因为且
且
因为


由正弦定理得



所以
解析
解析已在路上飞奔,马上就到!
知识点
7.年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人, 他们的健康状况如下表:
其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,-1代表“生活不能自理”.则随机访问该小区一位80岁以下的老龄人,该老人生活能够自理的概率是_____(用分数作答)。
正确答案
287/300
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数



正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
11.函数


正确答案
1/4
解析
解析已在路上飞奔,马上就到!
知识点
13.已知关于t的一元二次方程

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
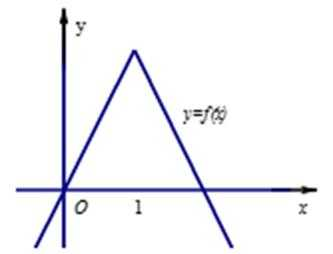
23.已知函数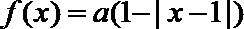
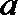
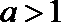
(1)求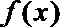
(2)证明函数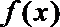
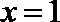
(3)当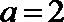
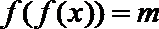
正确答案
(1)
当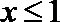
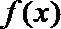
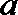
当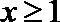
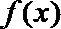
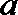
故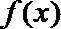
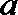
(2)设点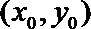
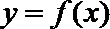
所以,函数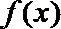
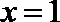
(3)当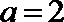
如图,
当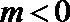
当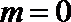
当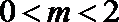
当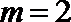
综合上述,
当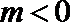
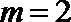
当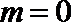
当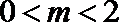
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.下列函数中周期为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析