- 函数的概念与基本初等函数
- 共5812题
8.设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设


(1)求
(2)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
(Ⅰ)试估计厨余垃圾投放正确的概率;
(Ⅱ)试估计生活垃圾投放错误额概率;
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为








正确答案
(Ⅰ)由题意可知:
(Ⅱ)由题意可知:
(Ⅲ)由题意可知:
因此当



解析
解析已在路上飞奔,马上就到!
知识点
20. 在平面直角坐标系






(Ⅰ)求椭圆
(Ⅱ)设直线




正确答案
(Ⅰ)因为椭圆


点



所以
所以椭圆

(Ⅱ)直线





因为直线


整理得



因为直线


整理得
综合①②,解得

所以直线


解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(Ⅰ)求k的值;
(Ⅱ)求
(Ⅲ)设



正确答案
(I)
由已知,

(II)由(I)知,
设



由



当


综上可知,


(III)由(II)可知,当




当



设


当



所以当


所以
综上,对任意

解析
解析已在路上飞奔,马上就到!
知识点
12.若函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设关于






(1)求实数
(2)若函数


(3)设函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 如图是用模拟方法估计圆周率

入( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
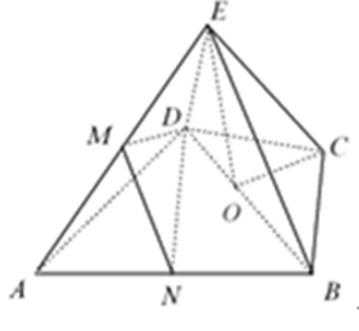
19.如图,几何体
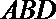
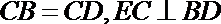
(Ⅰ)求证: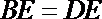
(Ⅱ)若∠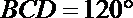
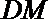
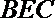
正确答案
(I)设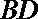
则由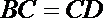
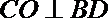
又已知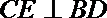
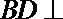
所以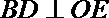
所以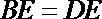
(II)取AB中点N,连接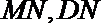
∵M是AE的中点,∴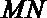

∵△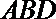
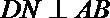
由∠BCD=120°知,∠CBD=30°,所以∠ABC=60°+30°=90°,即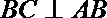
所以ND∥BC,
所以平面MND∥平面BEC,故DM∥平面BEC.
解析
解析已在路上飞奔,马上就到!
知识点
5.已知定义在R上的函数f(x)关于直线x=1对称,若f(x)=x(1-x)(x≥1),则f(-2)=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函y=f(x)定义在[-
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数f(x)=ax2+bx-1(a,b∈R且a>0)有两个零点,其中一个零点在区间(1,2)内,则a-b的取值范围为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数
正确答案
[0,+∞]
解析
解析已在路上飞奔,马上就到!
知识点
13.f(x)=(x2-3)ex(e为自然对数的底数)的最小值是 ( )。
正确答案
-2e
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析