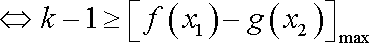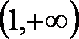- 函数的概念与基本初等函数
- 共5812题
已知数列






(1)若数列


(2)若




(3)若










正确答案
见解析
解析
(1)由题意得:




(2)证法一:
证明:由已知,

因此,猜想
① 当

② 假设

当
故当
由 ①、② 可知,对于任意正整数

设数列



由于

所以 

因此,数列

证法二:
因为 


…… 
由于




即

由于

根据“生成数列”的定义知,数列

(3)证法一:
证明:设数列





由(2)中结论可知 

所以,

所以
证法二:
因为 
所以 
所以欲证

对于数列

因为 


…… 
由于




相加得


设数列



所以 

同理可证,

所以 
知识点
已知函数f(x)=lnx-mx(mR)。
(1)若曲线y=f(x)过点P(1,-1),求曲线y=f(x)在点P处的切线方程;
(2)求函数f(x)在区间[1,e]上的最大值;
(3)若函数f(x)有两个不同的零点x1,x2,求证:x1x2>e2。
正确答案
见解析。
解析
(1)因为点P(1,-1)在曲线y=f(x)上,所以-m=-1,解得m=1.
因为
(2)因为
①当m≤0时, x∈(1,e), f ′(x)>0,所以函数f (x)在(1,e)上单调递增,则f (x) max=f (e)=1-me。
②当

f (e)=1-me,
③当



则f (x) max=
④当
综上,①当
②当
③当m≥1时,f (x)max=-m,
(3)不妨设x1>x2>0.因为f (x1)=f (x2)=0,所以lnx1-mx1=0,lnx2-mx2=0,
可得lnx1+lnx2=m(x1+x2),lnx1-lnx2=m(x1-x2)。
要证明x1x2>e2,即证明lnx1+lnx2>2,也就是m(x1+x2)>2。
因为


令

令


故函数(t)在(1,+∞)上是增函数,所以

所以原不等式成立,
知识点
记函数


设函数


令

(1)若函数


(2)当


(3)试写出

正确答案
见解析
解析
(1)
由题意
(2)当


显然g(x)在

故

从而:

(3)
1)当


此时,
2) 当


此时,
3) 当


4) 当


故
因





故当

知识点
设P是函数


正确答案
解析


故
知识点
已知函数


正确答案
解析
据已知关系式可得

知识点
某种树苗栽种时高度为A(A为常数)米,栽种n年后的高度记为f(n),经研究发现f(n)近似地满足 f(n)=,其中t=
(1)栽种多少年后,该树木的高度是栽种时高度的8倍;
(2)该树木在栽种后哪一年的增长高度最大,
正确答案
见解析。
解析
(1)由题意知f(0)=A,f(3)=3A。
所以
所以
令f(n)=8A,得

即
所以栽种9年后,该树木的高度是栽种时高度的8倍,
(2)由(1)知
第n年的增长高度为
所以
当且仅当64tn=,即
所以该树木栽种后第5年的增长高度最大,
知识点
若函数




(1)判断下列函数,是否为“
①
②
(2)已知函数


正确答案
见解析
解析
(1)若



即

而
因此

② 答案不唯一:如取


即存在实数对


一般地:若


即存在常数对



(2)函数

设有序实数对

当

因此

则有
即
所以
当
满足


知识点
已知函数


正确答案
解析
由
所以
所以
知识点
已知函数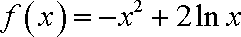
(1)求函数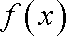
(2)若函数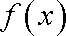
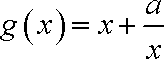
①求实数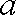
②若对于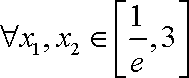

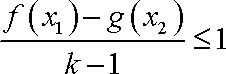
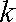
正确答案
见解析
解析
(1)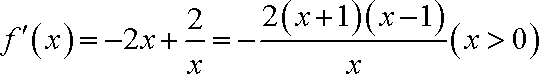
由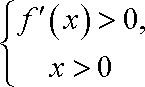
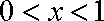
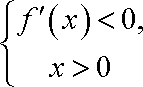

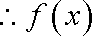
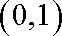
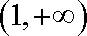


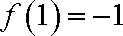
(2)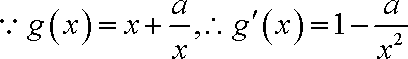
①由(1)知,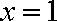
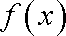
又
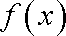
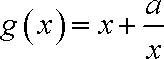
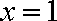

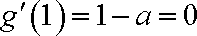
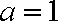
经验证,当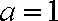
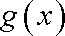
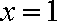
②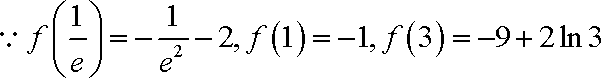
易知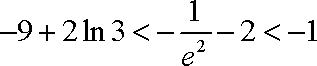
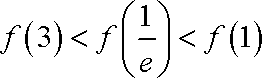
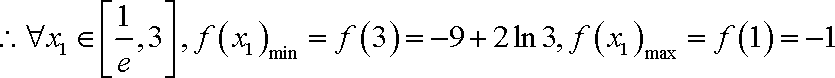
由①知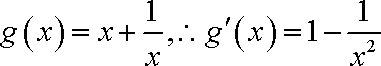
当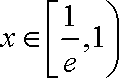
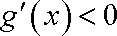

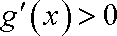
故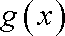
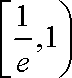
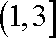
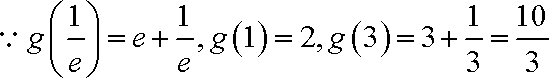
而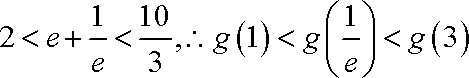
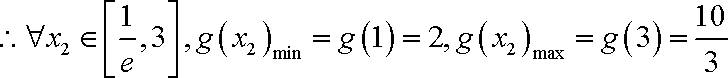
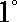
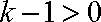

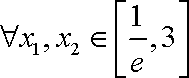
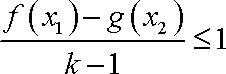
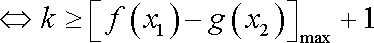
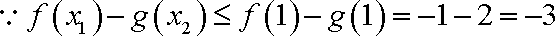
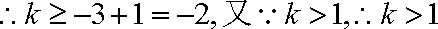

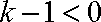

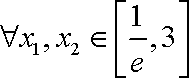
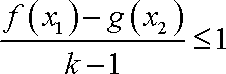
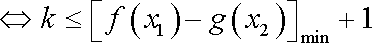
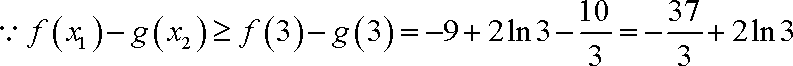
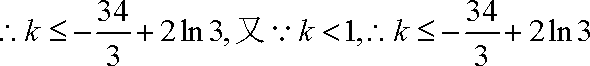
综上,所求实数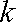
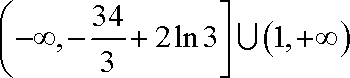
知识点
若
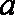
正确答案
解析
因为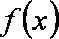
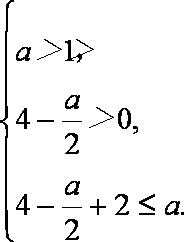
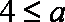
知识点
已知

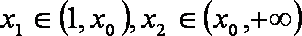
正确答案
解析
令
从而有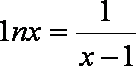


由
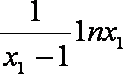
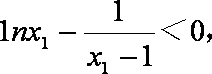
知识点
已知函数



(1)试判断
(2)解关于
正确答案
见解析。
解析
(1)




由

(2)由
又由(1)可得
即:
解得:

知识点
将函数y=sin(2x﹣
正确答案

解析
将函数y=sin(2x﹣
所得到的图象对应的函数解析式为y=sin[2(x+ϕ)﹣

再由y=sin(2x+2ϕ﹣


故答案为 
知识点
已知函数f(x)=

正确答案
[﹣
解析
作出函数f(x)=
将直线y=kx围绕坐标原点进行旋转,可得当直线介于与第二个半圆相切和与第三个半圆相切之间时,两图象有且仅有四个不同的公共点,
此时,其最大根t∈(

则函数g(t)=



故答案为:[﹣
知识点
已知函数
正确答案
3
解析
由
知识点
扫码查看完整答案与解析