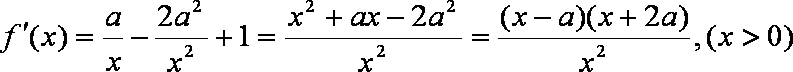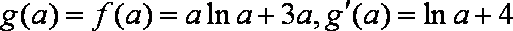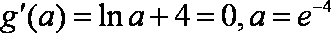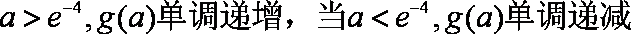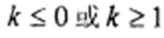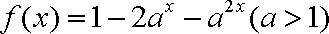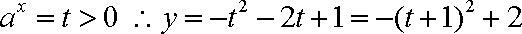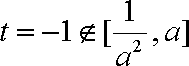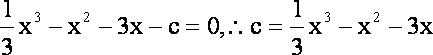- 函数的概念与基本初等函数
- 共5812题
已知二次函数

(1)若方程

(2)若
正确答案
见解析。
解析
(1)∵不等式
∴





又方程
∴△=
∴
∴


∴

(2)由(1)知





∵





∴所求实数a的取值范围是
知识点
已知函数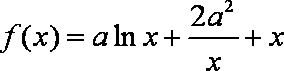
(1)若曲线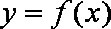
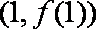
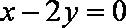
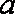
(2)若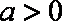
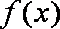
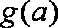
(3)在(2)上求证: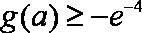
正确答案
见解析
解析
(1)
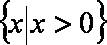
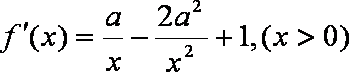
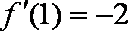
所以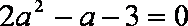
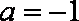
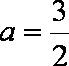
(2)
当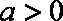
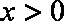
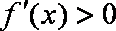
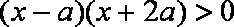
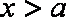
由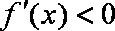
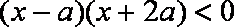
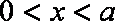
所以函数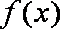
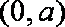
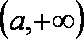
(3)由(2)知,当a>0, 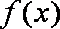
令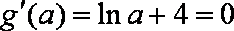
当
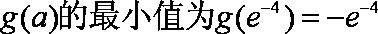
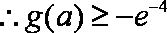
知识点
已知函数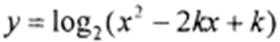
正确答案
解析
要满足题意,t=x2-2kx+k要能取到所有正实数,抛物线要与x轴有交点,
∴△=4k2-4k≥0.解得k≥1或k≤0.故选 C。
知识点
已知函数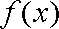
(1)求函数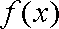
(2)当
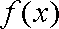
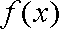
正确答案
见解析。
解析
设
(1)
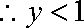

(2)
所以
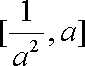

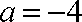
当
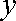
即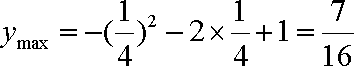
知识点
热力公司为某生活小区铺设暖气管道,为减少热量损耗,管道外表需要覆盖保温层。经测算要覆盖可使用20年的保温层,每厘米厚的保
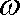

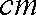
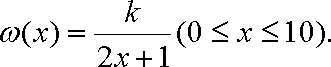
(1)求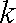
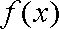
(2)问保温层多厚时,总费用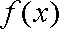
正确答案
见解析。
解析
(1)由题意知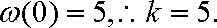
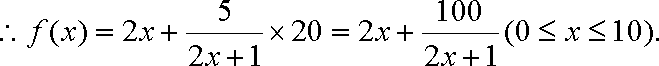
(2)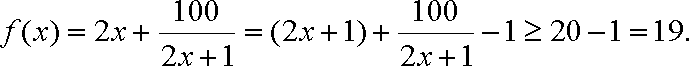
当且仅当
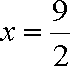
所以保温层的厚底为
知识点
已知函数f(x)=
正确答案
见解析。
解析
∵f(1)=2
∴a+1=2b……………………5分
∵f(2) <3
∴-1<a<2……………………8分
∵a,b,c∈Z
∴a=0或a=1…………………………10分
当a=0时,b=
当a=1时,b=1,c=0…………………………12分
知识点
某公司计划投资

(1)分别将

(2)该公司已有10万元资金,并全部投入

正确答案
见解析。
解析
(1)设投资


依题意可设
由图1,得

由图2,得

故
(1)设B产品投入


由(1)得





因此当A产品投入6万元,B产品投入4万元时,该企业获得最大利润为2.8万元。(12分)
知识点
函数
正确答案
解析
因为


知识点
函数
正确答案
解析
将题目简化下,原函数与|x-1|+|x-2|+|x-3|的图像性质类似可以用图像,做一条x轴,标出1,2,3的坐标函数的集合意义即x轴上的点到3个点的距离和然后分x在1点左方,1和2之间,2和3之间,3点右方来讨论不难得出上述结论。其对称轴为x=1006,在对称轴的右方单调递增,左方单调递减。
知识点
某地区的农产品A第





(1)求该农户在第7天销售家产品A的收
(2)问这20天中该农户在哪一天的销售收入最大?
正确答案
见解析。
解析
(1)由已知第7天的销售价格

所以第7天的销售收入
(2)设第


当

当且仅当


当

当且仅当


由于
所以第2天该农户的销售收入最大.……………………………………………………12分
知识点
定义在

① 


② 
③ 


(1)求函数
(2)设



正确答案
见解析。
解析
(1)



∴
由

又



由①②③得:

(2)由已知得:若存在



设

令


当



当



∴

又


于是有
知识点
设函数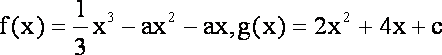
(1) 试问函数
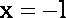
(2) 若a=-1,当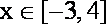
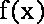
正确答案
见解析。
解析
(1)由题意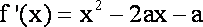
假设在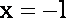

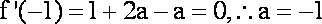
而此时,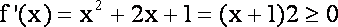
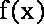
这与

(2)设
设
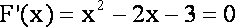
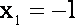
列表如下:
知识点
已知函数

(1)如果函数


(2)是否存在正实数



正确答案
见解析。
解析
(1)当


当


由于




综上,


(2)
因


即方程

设


令



当


当


为满足题意,只需

解得
知识点
已知

(1)若



(2)求
正确答案
见解析。
解析
(1)


又当
所以曲线

(2)解:令

当


当


当




增。
从而 
故函数

知识点
已知

(1)讨论

(2)求证:在(1)的条件下,
(3)是否存在实数


正确答案
见解析。
解析
(1)
∴当


当


∴

(2)


∴ 
令

当



∴
∴在(1)的条件下,
(3)假设存在实数

① 当



所以,此时
②当





③ 当

所以


所以,此时
综上,存在实数


知识点
扫码查看完整答案与解析