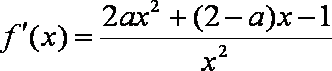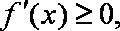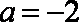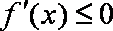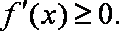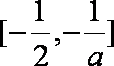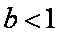- 函数的概念与基本初等函数
- 共5812题
设函数



(1)求数列
(2)是否存在等比数列


正确答案
见解析。
解析
(1)由

得


即 
即 
即
∵



由①得,

因此 ,数列

(2)假设存在等比数列


当

③-④,得 
由

又
因此,存在等比数列


知识点
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在直线与海岸线,的夹角为60°(海岸线看作直线),跑道上距离海岸线最近的点B到海岸线的距离BC=4


(1)将tan
(2)求点D的位置,使得
正确答案
见解析
解析
(1)过A分别作直线CD、BC的垂线,垂足分别为E,F.
由题设知,∠ABF=30°,∴
又

∴

即
(2)记


而
∴


函数


而



答:在海岸线l上距离C点6km处的D点观看飞机跑道的视角最大,………………………13分
知识点
在




正确答案
解析
由

即





知识点
在平面直角坐标系xOy中,已知点







正确答案
解析
易得


知识点
设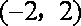
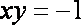

正确答案
解析
易得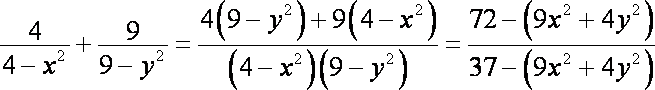
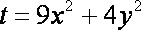
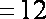
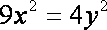
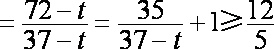
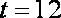
成立);
知识点
已知函数
(1)求

(2)求


(3)对任意给定的正实数






正确答案
见解析
解析
(1)因为
当

解









(2)①当






又


②当














(3)假设曲线








因为


即:
是否存在点
若


若


设









所以,对任意给定的正实数





知识点
某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交




(1)求分公司一年的利润L(万元)与每件产品的售价
(2)当每件产品的售价为多少元时,分公司一年的利润L最大?并求出L的最大值
正确答案
见解析。
解析
(1)分公司一年的利润L(万元)与售价

(2)
令


∵
在




(2)当


所以
答:若




知识点
设函数
(1)当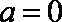
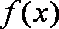
(2)设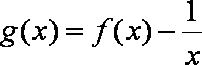
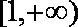
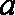
(3)当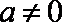
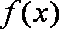
正确答案
见解析。
解析
(1)函数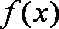
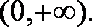
当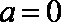
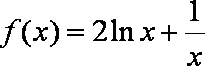
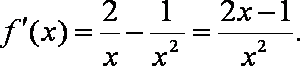
由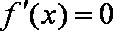
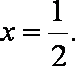
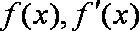
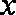
故,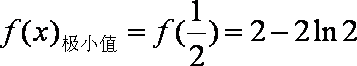
(2)由题意,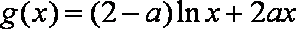
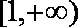
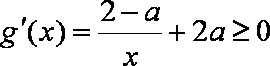
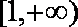
设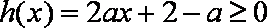
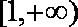
当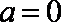
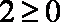
当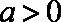
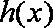
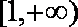
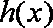
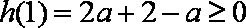
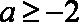
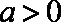
当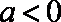
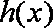
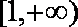
所以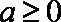
(3)由题意,
令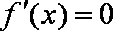


若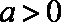
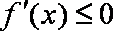
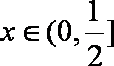
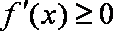
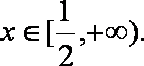
若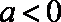
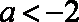
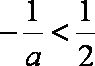
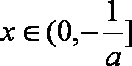

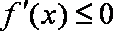
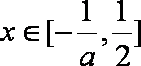
②当
③当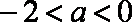
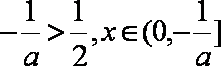

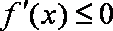
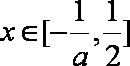
综上,当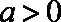
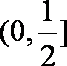
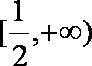
当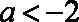
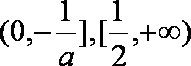
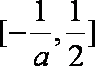
当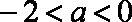
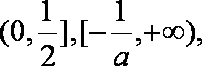
………………
知识点
已知函数







正确答案
10
解析
由题设知,




知识点
已知电流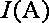
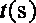
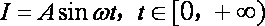
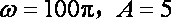
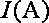
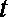
正确答案
解析
易得周期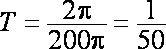
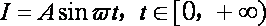
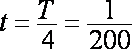
知识点
记定义在


(1)当

(2)直接写出
(3)在所有形如题设的函数


正确答案
见解析。
解析
(1)当


所以
此时,
(2)由(1)同理可得,
(3)记



①若


所以

②若





所以




所以


由



综上所述,所有形如题设的函数
知识点
已知函数f(x)=lnx﹣ax2﹣x,a∈R。
(1)若函数y=f(x)在其定义域内是单调增函数,求a的取值范围;
(2)设函数y=f(x)的图象被点P(2,f(2))分成的两部分为c1,c2(点P除外),该函数图象在点P处的切线为l,且c1,c2分别完全位于直线l的两侧,试求所有满足条件的a的值。
正确答案
见解析
解析
解:(1)
只需要2ax2+x﹣1≤0,即
所以
(2)因为
所以切线l的方程为
令

若a=0,则
当x∈(0,2)时,g'(x)>0;当x∈(2,+∞)时,g'(x)<0,
所以g(x)≥g(2)=0,c1,c2在直线l同侧,不合题意;
若a≠0,
若

当x∈(2,+∞)时,g(x)>g(2)=0;当x∈(0,2)时,g(x)<g(2)=0,符合题意;
若

当x∈(2,+∞)时,g'(x)>0,g(x)>g(2)=0,不合题意;
若

当x∈(0,2)时,g'(x)>0,g(x)<g(2)=0,不合题意;
若a>0,当x∈(0,2)时,g'(x)>0,g(x)<g(2)=0,
当x∈(2.+∞)时,g'(x)<0,g(x)<g(2)=0,不合题意。
故只有
知识点
已知函数
正确答案
解析
解:∵ f(x)=
由图可知,当a=1时,直线y=



∴ bf(a)=


当b=1时,直线y=3与f(x)只有一个交点,且f(a)=f(b)=3,
∴ bf(a)=1×3=3,
∴ bf(a)的取值范围为[
知识点
已知函数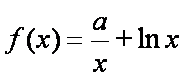
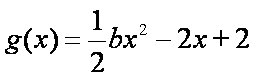

(1)求函数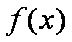
(2)记函数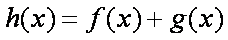
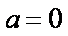
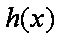
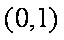

(3)记函数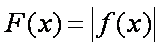
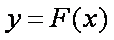
正确答案
见解析
解析
(1)因为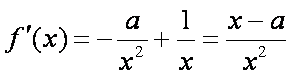
①若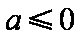
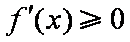
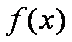
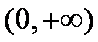
②若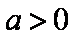
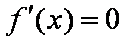
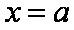
当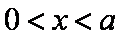
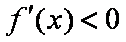
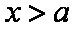
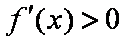
所以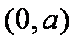
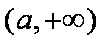
综上可得,当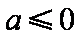
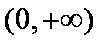
当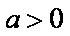
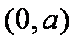
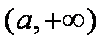
(2)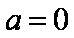
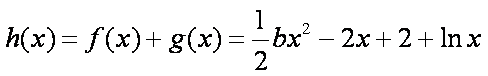
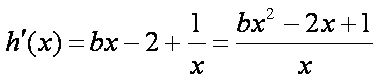
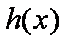
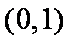
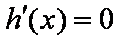
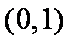
由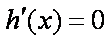
(i)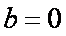
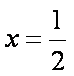
(ii)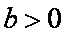
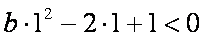
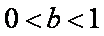
(iii)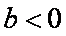
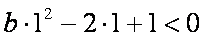
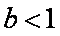
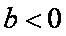
综上得: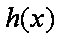
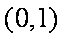
注:本题也可分离变量求得。
(3)证明:由(1)可知:
(i)若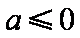
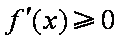
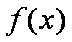
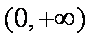
所以直线
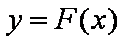
(ⅱ)若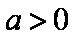
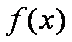
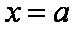
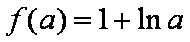
若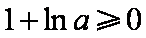

故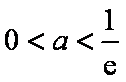
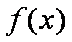
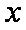
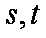
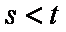
则直线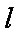
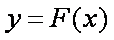
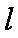
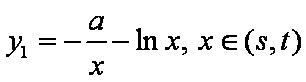
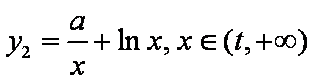
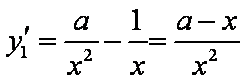
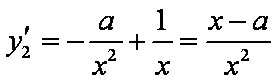
设切点分别为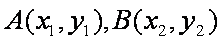

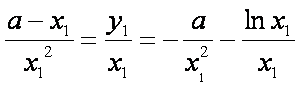
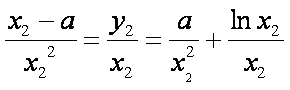
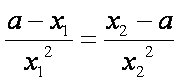
即

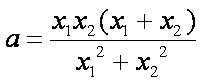
①-②得: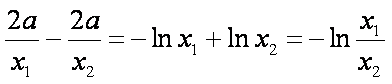
由③中的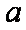
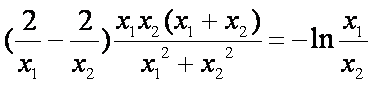
即
令
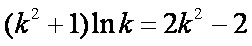
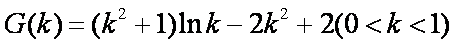
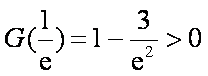
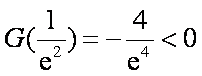
故存在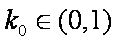
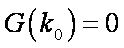
即存在一条过原点的直线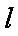
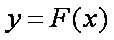
知识点
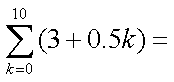
正确答案
解析
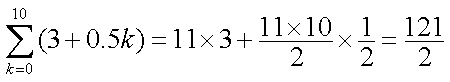
知识点
扫码查看完整答案与解析