- 函数的概念与基本初等函数
- 共5812题
已知定义在R上的函数y=f（x）满足一下三个条件：
①对于任意的x∈R，都有f（x+4）=f（x）；
②对于任意的x1，x2∈R，且0≤x1≤x2≤2，都有f（x1）＜f（x2）；
③函数的图象关于x=2对称；
则下列结论中正确的是（ ）
正确答案
解析
由①③两个条件得：f（4.5）=f（0.5）；f（7）=f（3）=f（1）；f（6.5）=f（2.5）=f（1.5），
根据条件②，0≤x1＜x2≤2时，都有f（x1）＜f（x2）；
∴f（0.5）＜f（1）＜f（1.5），
∴f（4.5）＜f（7）＜f（6.5）。
知识点
函数f（x）=lnx﹣x+2的零点个数为
正确答案
2
解析
∵f（x）=lnx﹣x+2=0
∴x﹣2=lnx
令y1=lnx，y2=x﹣2
根据这两个函数的图象在同一个坐标系中的位置关系知，
两个图象有两个公共点，
∴原函数的零点的个数是2
知识点
函数
A
B
C
Dx=π
正确答案
解析
y=2sin（x+
令2x=2kπ+
则k=1时，x=
知识点
己知函数f（x）是定义在R上的偶函数，且对任意的x∈R，都有f（x+2）=f（x），当0≤x≤1对，f（x）=x2，若直线y=x+a与函数y=f（x）的图象在[0，2]内恰有两个不同的公共点，则实数a的值是（ ）
A0
B0或
C0或
D
正确答案
解析
由对任意的x∈R，都有f（x+2）=f（x）可知，函数的周期为T=2，
结合函数为偶函数，且当0≤x≤1对，f（x）=x2可作出函数y=f（x）和直线y=x+a的图象，
当直线为图中的直线m，n时，满足题意，易知当直线为m时，过原点，a=0，
当直线为n时，直线与曲线相切，联立
由△=1+4a=0可得a=
知识点
在△ABC中，∠A=90°，AB=1，AC=2，设点P，Q满足
正确答案
解析
∵
又∵
∴
∵∠A=90°，得
∴
展开并化简得，﹣（1﹣λ）
∵|
∴﹣（1﹣λ）×4﹣λ×1=﹣2，解之得
知识点
已知
正确答案
解析
∵0＜a=log32＜log33=1；
b=
c=
∴b＞a＞c。
知识点
设函数f（x）=ex﹣ax﹣2
（1）求f（x）的单调区间
（2）若a=1，k为整数，且当x＞0时，（x﹣k） f´（x）+x+1＞0，求k的最大值。
正确答案
见解析。
解析
（1）函数f（x）=ex﹣ax﹣2的定义域是R，f′（x）=ex﹣a，
若a≤0，则f′（x）=ex﹣a≥0，所以函数f（x）=ex﹣ax﹣2在（﹣∞，+∞）上单调递增。
若a＞0，则当x∈（﹣∞，lna）时，f′（x）=ex﹣a＜0；当x∈（lna，+∞）时，f′（x）=ex﹣a＞0；所以，f（x）在（﹣∞，lna）单调递减，在（lna，+∞）上单调递增。
（2）由于a=1，所以，（x﹣k） f´（x）+x+1=（x﹣k） （ex﹣1）+x+1
故当x＞0时，（x﹣k） f´（x）+x+1＞0等价于k＜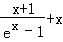
令g（x）=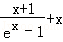
由（1）知，函数h（x）=ex﹣x﹣2在（0，+∞）上单调递增，而h（1）＜0，h（2）＞0，所以h（x）=ex﹣x﹣2在（0，+∞）上存在唯一的零点，故g′（x）在（0，+∞）上存在唯一的零点，设此零点为α，则有α∈（1，2）
当x∈（0，α）时，g′（x）＜0；当x∈（α，+∞）时，g′（x）＞0；所以g（x）在（0，+∞）上的最小值为g（α），又由g′（α）=0，可得eα=α+2所以g（α）=α+1∈（2，3）
由于①式等价于k＜g（α），故整数k的最大值为2
知识点
如图，已知AB为圆O的直径，AC与圆O相切于点A，CE∥AB交圆O于D、E两点，若AB=2，CD=
正确答案
解析
设CD=
∵AC与圆O相切于点A，∴AC⊥AB，AC2=CD•CE=
∴AD2=AC2+CD2=
∵CE∥AB，∴
故答案为
知识点
已知函数f（x）=x﹣
（1）求函数f（x）的单调区间：
（2）求f（x）在区间[1，e2]上的值域；
（3）若函数g（x）=7f（x）+m﹣
正确答案
见解析。
解析
（1）函数f（x）的定义域为（0，+∞）。
∴当x∈（0，1）时，f′（x）＞0，f（x）为增函数。
当x∈（1，2）时，f′（x）＜0，f（x）为减函数。
当x∈（2，+∞）时，f′（x）＞0，f（x）为增函数。
∴f（x）的增区间为（0，1）（2，+∞），
减区间为（1，2）；
（2）由（1）可知在区间（1，e2）内，当x=2时，f（x）取得极小值，
而f（1）=0，f（2）=2﹣3ln2，
∵f（2）＜f（1）＜f（e2），
∴f（x）在区间（1，e2）上的值域为
（3）由
得
∴
当x∈[1，2）时，g′（x）＞0，g（x）在[1，2）上单调递增；
当x∈（2，4]时，g′（x）＜0，g（x）在（2，4]上单调递减。
则g（x）在[1，4]上有最大值g（x）max=g（2）=m﹣2ln2﹣2=3。
∴实数m的值为5+2ln2。
知识点
函数f（x）=ex+x﹣2的零点所在区间是（ ）
正确答案
解析
∵函数f（x）=ex+x﹣2，∴f（0）=1+0﹣2=﹣1＜0，f（1）=e+1﹣2=e﹣1＞0，故有f（0）f（1）＜0，
根据函数零点的判定定理可得 函数f（x）=ex+x﹣2的零点所在区间是（0，1），
知识点
函数
A-1
B
C
D0
正确答案
解析
试题分析：因为
知识点
函数
A
B0
C
D
正确答案
解析
试题分析：当
知识点
设
A
B
C
D2
正确答案
解析
试题分析：
即
即
设
知识点
函数
A2，
B2，
C4，
D4，
正确答案
解析
试题分析：由题意得：
知识点
设定义域为R的函数
正确答案
解析
试题分析： 
由图可知，只有当
故关于
知识点
扫码查看完整答案与解析