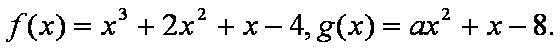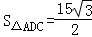- 函数的概念与基本初等函数
- 共5812题
已知函数
(1)求函数
(2)求函数
正确答案
见解析
解析
(1)因为f(x)=

所以函数f(x)的最小正周期为2π
(2)令
得
故函数f(x)的单调增区间为[2kπ-

知识点
已知函数



(1)求
(2)求函数
(3)0设函数

正确答案
见解析
解析
(1)设
则:



(2)

所以



(3)

若函数



即



则

所以函数


知识点
已知函数
(1)若函数


(2)若函数


(3)在(1)的条件下,判断过点

正确答案
见解析
解析
(1)
∵ 


∴ 


∴ 

∴ 
(2)若函数

则
∴ 

∴ 
(3)

则


∴ 切线的斜率为

设
由


∴


∴ 函数


∵ 

∴ 方程
∴ 过点

知识点
已知



(1)当


(2)求函数

(3)若在区间



正确答案
见解析。
解析
由

(1)当

所以

(2)令
(1) 当

故


(2)当


所以

(3)设
对

因为





依题意,只需

即

所以正实数

知识点
设函数


(1)若直线




(2)若函数

正确答案
见解析。
解析
(1)由


由


(i)当
(ii)当



(2)
(i)若函数








(ii)若函数








综上可得,若函数


知识点
已知函数
(1)求函数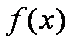
(2)若对任意的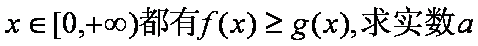
正确答案
见解析
解析
解:(1)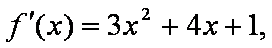
令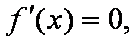
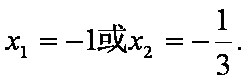
当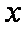
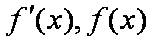
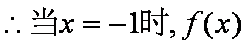

(2)设
若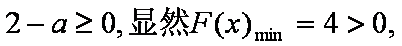
若
令
当
当
即
解不等式得:
当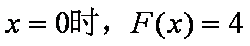
综上所述
知识点
函数




正确答案
解析
当










当









综上所述,
知识点
已知函数

(1)若函数



(2)当

正确答案
见解析
解析
(1)函数




(2)令

若


若

∴当



∴


∴
又∵

∴
∴

综上,当

知识点
设变量x、y满足约束条件
正确答案
解析
设变量x、y满足约束条件
在坐标系中画出可行域△ABC,A(2,0),B(1,1),C(3,3),
则目标函数z=2x+y的最小值为3。
知识点
已知函数f(x)=x3﹣tx2+3x,若对于任意的a∈[1,2],b﹣a=1,函数f(x)在区间(a,b)上单调递减,则实数t的取值范围是( )
正确答案
解析
f′(x)=3x2﹣2tx+3,
因为f(x)在区间(a,b)上单调递减,
所以f′(x)≤0即3x2﹣2tx+3≤0在(a,b)上恒成立,
所以有

所以
因为对于任意的a∈[1,2],f(x)在(a,b)上单调递减,所以(*)式恒成立,
又

所以
知识点
把函数y=sin(x+


正确答案
解析
把函数y=sin(x+



再将所得图象的横坐标变为原来的
令2kπ﹣



故所得函数的增区间为[

知识点
己知函数f(x)是定义在R上的偶函数,且对任意的x∈R,都有f(x+2)=f(x),当0≤x≤1对,f(x)=x2,若直线y=x+a与函数y=f(x)的图象在[0,2]内恰有两个不同的公共点,则实数a的值是( )
正确答案
解析
由对任意的x∈R,都有f(x+2)=f(x)可知,函数的周期为T=2,
结合函数为偶函数,且当0≤x≤1对,f(x)=x2可作出函数y=f(x)和直线y=x+a的图象,
当直线为图中的直线m,n时,满足题意,易知当直线为m时,过原点,a=0,
当直线为n时,直线与曲线相切,联立
由△=1+4a=0可得a=

故选C
知识点
已知函数f(x)=ax2﹣ex(a∈R),f′(x)是f(x)的导函数(e为自然对数的底数)。
(1)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若f(x)有两个极值点x1,x2,求实数a的取值范围;
(3)若当x≥0时,不等式f(x)≤﹣x﹣1恒成立,求实数a的最大值
正确答案
见解析。
解析
(1)由题意得,当a=1时,f(x)=x2﹣ex,
∴f′(x)=2x﹣ex,则切线的斜率为f′(0)=﹣1,
∵f(0)=﹣e0=﹣1,
∴所求的切线方程为:x+y+1=0;
(2)设g(x)=f′(x)=2ax﹣ex,
由题意得,x1,x2是方程g(x)=0(即2ax﹣ex=0)的两个实根,
则g′(x)=2a﹣ex,
当a≤0时,g′(x)<0,g(x)在定义域上递减,即方程g(x)=0不可能有两个实根,
当a>0时,由g′(x)=0,得x=ln2a,
当x∈(﹣∞,ln2a)时,g′(x)>0,则g(x)在(﹣∞,ln2a)上递增,
当x∈(ln2a,+∞)时,g′(x)<0,则g(x)在(﹣∞,ln2a)上递减,
∴gmax(x)=g(ln2a)=2aln2a﹣2a,
∵方程g(x)=0(即2ax﹣ex=0)有两个实根,
∴2aln2a﹣2a>0,解得2a>e即
(3)设h(x)=ex﹣ax2﹣x﹣1,则由题意得h(x)=ex﹣ax2﹣x﹣1≥0在[0,+∞)恒成立,
则h′(x)=ex﹣2ax﹣1,
当a=0时,h′(x)≥0,h(x)在[0,+∞)上单调递增,
∴h(x)≥h(0)=0,即ex≥1+x,当且仅当x=0时,等号成立,
∴h′(x)=ex﹣2ax﹣1≥1+x﹣2ax﹣1=x(1﹣2a),
当1﹣2a≥0时,即a≤
∴h(x)≥h(0)=e0﹣0﹣1=0,即h(x)≥0,
因而a≤
下面证明a>
由ex≥1+x得,e﹣x≥1﹣x,即x≥1﹣e﹣x,
∴h′(x)=ex﹣1﹣2ax≤ex﹣1﹣2a(1﹣e﹣x)=e﹣x(ex﹣1)(ex﹣2a)
当ex<2a时,即0<x<ln2a,则当x∈(0,ln2a)时,h′(x)<0,从而h(x)<0,
因此,对于x≥0,f(x)≤﹣x﹣1不恒成立,
综上所得,a的最大值为
知识点
如图,在四边形ABCD中,AC平分∠DAB,已知∠B=60°,AC=7.AD=6,面积
(1)求sin∠DAC和cos∠DAB的值;
(2)求边BC,AB的长度。
正确答案
见解析。
解析
(1)∵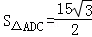
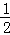
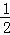
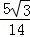
再由AC平分∠DAB,可得∠DAB=2∠DAC,∴cos∠DAB=cos2∠DAC=1﹣2sin2∠DAC=1﹣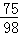
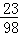
(2)△ABC中,sin∠BAC=sin∠DAB=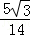
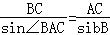
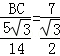
再由余弦定理可得 BC2=AB2+AC2﹣2AB•AC•sin∠BAC,即 25=AB2+49﹣14AB•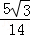
解得 AB=8,或 AB=﹣3(舍去)。
综上,AB=8,BC=5
知识点
已知函数
(1)当


(2)如果函数


(3)当

正确答案
(1)

解析
(1)当


所以

所以切线方程为
(2)因为

等价于

变形得

而
(当且仅当

所以
(3)
令

所以

(ⅰ)当


(ⅱ)当


(ⅲ)当

① 因为


② 
设

因为



所以



所以

综上所述:当

当

当

知识点
扫码查看完整答案与解析