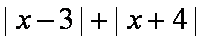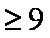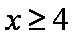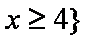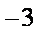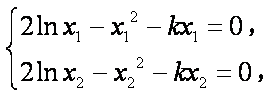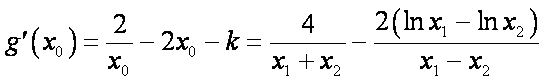- 函数的概念与基本初等函数
- 共5812题
已知函数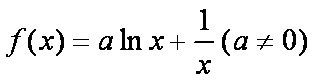
(1)求函数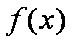
(2)若存在两条直线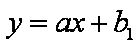
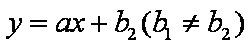

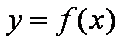
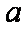
(3)若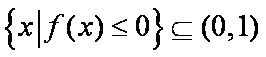
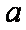
正确答案
见解析
解析
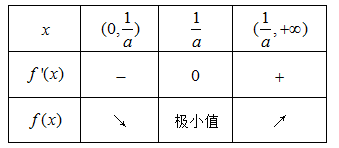
(1)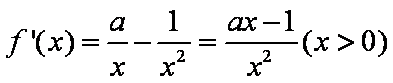
当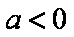
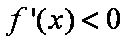
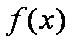
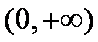
当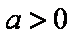
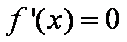
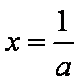
当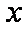
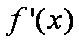
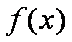
所以 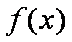
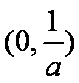

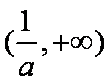
(2)因为 存在两条直线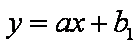
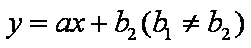
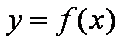
所以 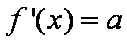
令
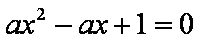
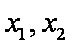
则 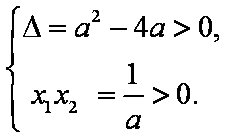
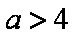

当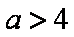
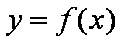
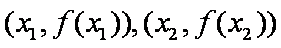
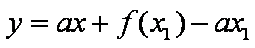

令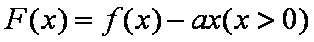
由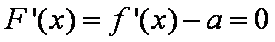
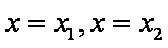
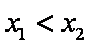
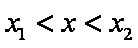
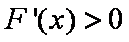
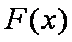
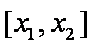
所以 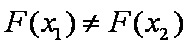
所以 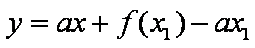
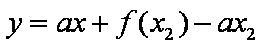
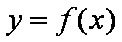
所以 实数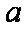
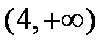
(3)当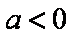
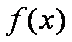
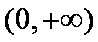
因为 
而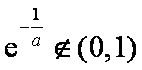

当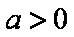
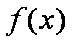
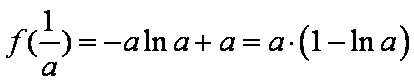
(ⅰ)若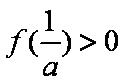
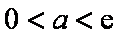
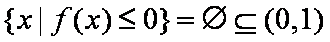
所以,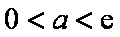
(ⅱ)若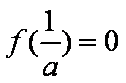

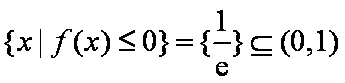
所以,
(ⅲ)若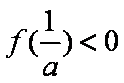
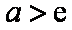

因为 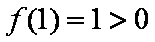
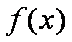
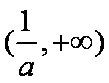
所以 当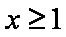

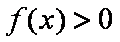
又因为 函数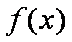
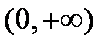
所以 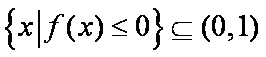
所以 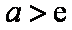
综上所述,实数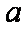
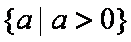
知识点
已知函数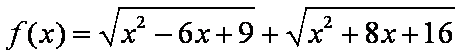
(1)求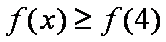
(2)设函数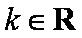
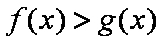
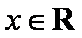
正确答案
见解析
解析
解:(1)
∴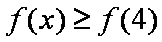
∴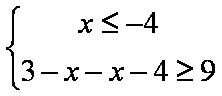
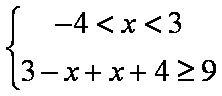
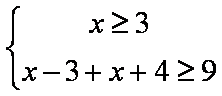
解得不等式①: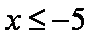
所以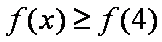
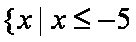
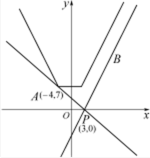
(2)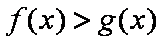
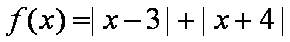
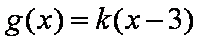
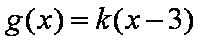
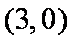
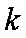
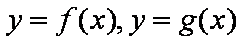
其中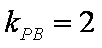
由图可知,要使得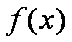
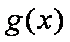
∴实数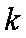
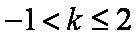
知识点
已知函数

(1)当a=2时,求函数
(2)当a>0时,求函数
(3)若函数




正确答案
见解析。
解析
(1)当a=2时,
则


(2)



①当




②当



由


由

综上,当


当




(3)函数

由




由


h(x)单调递减,所以
故实数m的取值范围是m≤
知识点
已知关于x的函数
(1)当

(2)若函数

正确答案
见解析
解析
解:(1)

当


所以,当


(2)
①当

因为F(1)=1>0,
若使函数F(x)没有零点,需且仅需
所以此时
②当

因为

所以此时函数
(或:当
当

由于
得




综上所述,所求实数a的取值范围是
知识点
定义在




正确答案
解析
略
知识点
设

正确答案
-1
解析
略
知识点
已知函数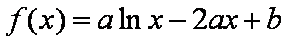
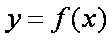

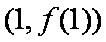
(1)求a,b的值。
(2)问:m在什么范围取值时,对于任意的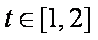
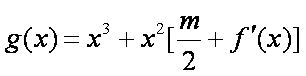
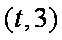
正确答案
见解析
解析
(1) 因为函数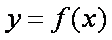
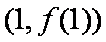
所以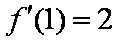
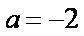
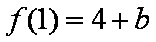
(2) 
因为任意的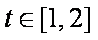
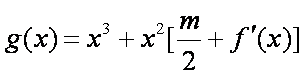
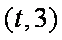
又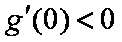
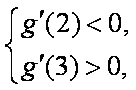
解得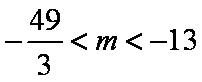
知识点
函数





① 函数
②函数
③ 若



④ 若函数

其中真命题是
正确答案
⑤
解析
略
知识点
函数
正确答案
解析
略
知识点
以下判断正确的是
正确答案
解析
略
知识点
设函数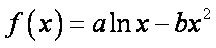
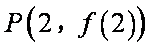
(1)求函数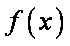
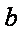
(2)当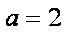
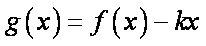
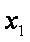
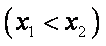
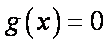
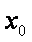
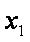
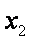
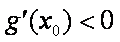
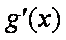
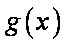
正确答案
见解析
解析
(1)函数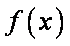
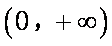
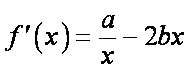
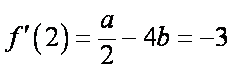
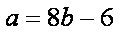
于是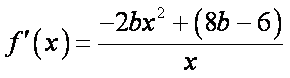
① 当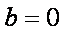
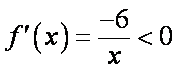
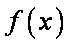
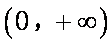
② 当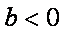
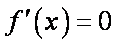
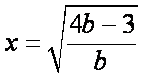
所以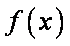
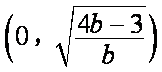
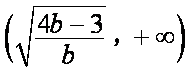
③ 当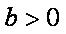
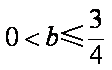
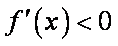
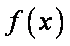
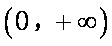
若
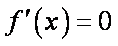
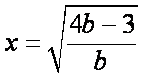

所以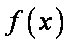
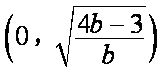
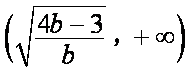
综上,若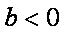
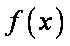

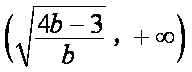
若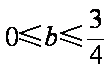
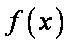
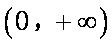
若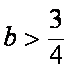
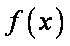
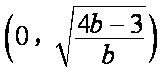
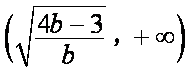
(2)因为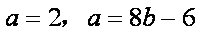
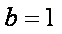
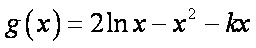
因为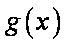
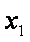
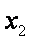
相减得: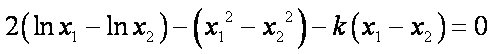
因为 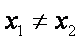
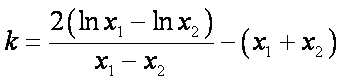
于是
令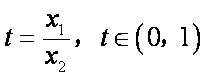
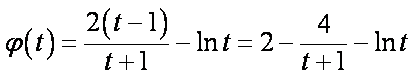
则
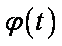
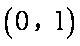
则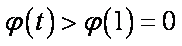
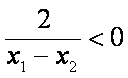
知识点
已知函数f(x)满足f(x)十f(-x) = 0,现将函数f(x)的图像按照

正确答案
解析
由函数







知识点
已知函数



正确答案
解析
略
知识点
已知函数f(x)= (1+tanx)cos2x的定义域为(0, 
正确答案
解析

因为

所以

知识点
如果一个棱柱的底面是正多边形,并且侧棱与底面垂直,这样的棱柱叫做正棱柱.已知一个正六棱柱的各个顶点都在半径为3的球面上,则该正六棱柱的体积的最大值为
正确答案
54
解析
设棱柱高为
则底面积

令

则
知识点
扫码查看完整答案与解析