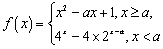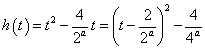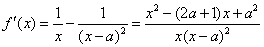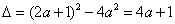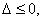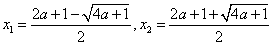- 函数的概念与基本初等函数
- 共5812题
定义:对于函数








(1)证明函数

(2)试判断函数




(3)设函数






正确答案
见解析
解析
(1)

所以函数
(2)函数


是广义周期函数, 且
(非零常数)。 -------------------------------------------------------------------------------------( 8分)
(3)
所以

设

由

又








由


又







知识点
函数

正确答案
解析
略
知识点
设某商品的需求函数为






正确答案
解析
略
知识点
已知函数
(1) 若


(2) 若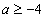



正确答案
见解析。
解析
(1) 因为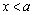
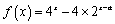
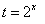
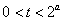
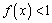
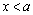
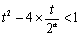
即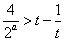
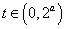
令p (t)=t-,
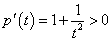
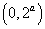
所以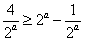
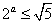
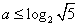
(2) 当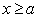
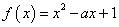
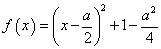
当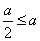
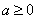
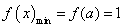
当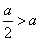
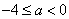
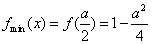
当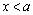
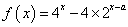
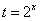
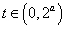
当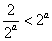
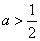
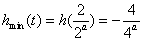
当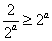
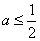
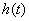
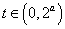
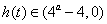
无最小值;
综合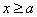
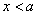
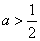
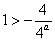
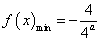
当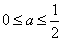
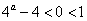
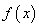
当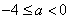
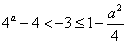
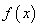
综上所述,当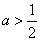
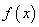
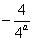
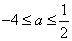
知识点
函数
正确答案
解析
略
知识点
已知函数
(1)当


(2)讨论函数
正确答案
见解析
解析
函数


(1) 当


所以曲线


(2)
(i)当



(ii)当



当


此时,


(iii)当



当


此时,


知识点
已知函数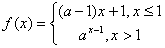
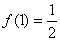
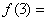
正确答案
解析
因为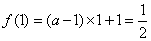
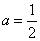
则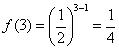
知识点
已知函数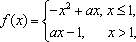
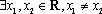
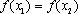

正确答案
解析
略
知识点
将函数

正确答案
解析



知识点
已知函数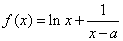
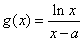
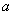
(1)求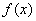
(2)若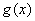
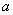
正确答案
见解析。
解析
(1)
设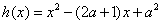
①当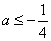
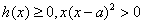
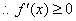
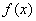
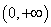
当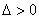
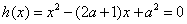
②当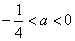
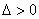
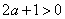
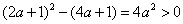
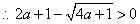
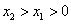
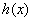
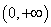
在区间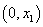
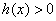
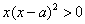
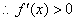
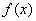
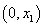
在区间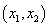
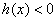
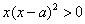
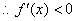
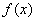
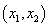
在区间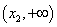
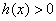
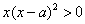
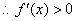
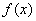
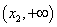
③当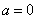
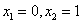
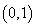
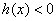
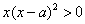
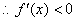
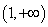
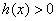
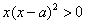
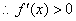
④当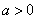
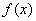
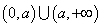
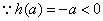
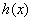
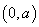
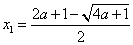
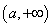
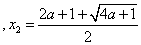
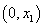
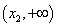
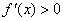
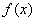
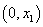
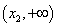
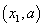
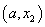
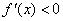
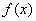
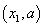
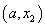
综上: 当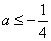
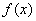
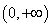
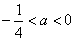
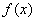
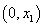
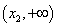
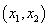
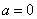
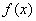
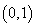
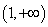
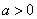
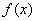
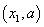
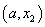
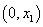
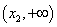
⑵当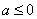
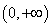
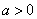
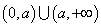
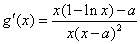
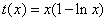
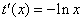
在区间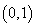
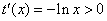
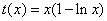
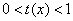
在区间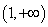
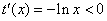
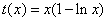
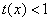
当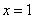
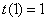
故当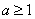
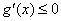
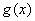
当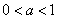
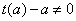
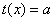
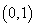
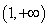
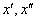
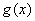
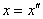
当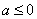
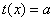
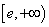
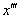
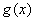
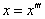
综上所述,若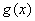
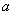
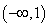
知识点
函数


正确答案
解析
略
知识点
下列函数中,在(0,+∞)上单调递增的偶函数是( )
正确答案
解析
y=cosx是偶函数,但在(0,+∞)上有增有减,故排除A;
y=x3在(0,+∞)上单调递增,但为奇函数,故排除B;
y=y=
y=ex+e﹣x是偶函数,由于y′=ex﹣e﹣x,在(0,+∞)上,y′>0,故其在(0,+∞)上单调递增的;正确。
故选D。
知识点
在极坐标系中,圆ρ=2上的点到直线
正确答案
1
解析
圆ρ=2 即x2+y2=4,圆心为(0,0),半径等于2.
直线 


圆心到直线的距离等于 
故答案为 1。
知识点
已知定点









正确答案


解析
略
知识点
已知函数
(1)求
(2)在







正确答案
(1)

(2)
解析
(1)


由

所以 


(2)因为 


因为 


因为 


因为 



所以 
知识点
扫码查看完整答案与解析