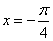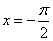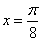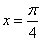- 函数的概念与基本初等函数
- 共5812题
已知定义在
A
B
C
D
正确答案
解析
略
知识点
设f（x）与g（x）是定义在同一区间［a，b］上的两个函数，若函数y＝f（x）－g（x）在[来源:Zxxk.Com]
x
称为“关联区间”，若f（x）＝x2－3x＋4与g（x）＝2x＋m在［0,3］上是产“关联函数”，则m的
取值范围为
A
B［－1,0］
C
D
正确答案
解析
略
知识点
已知函数
（1）当a＝1时，
（2）若在区间（1，＋
正确答案
见解析。
解析
知识点
函数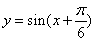
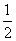
A
B
C
D
正确答案
解析
略
知识点
在
正确答案
解析
略。
知识点
已知函数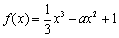
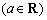
（1）若曲线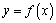
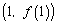
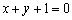
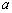
（2）若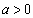
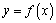
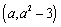
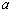
（3）若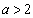
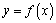
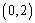
正确答案
见解析
解析
（1）解：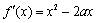
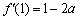
因为曲线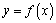
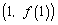
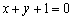
所以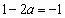
所以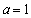
（2）解：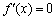
即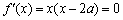
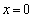
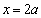
因为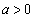
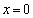
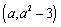
要使函数在区间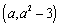
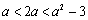
所以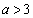
（3）证明：令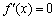
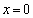
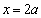
因为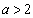
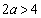
所以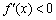
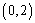
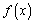
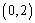
又因为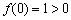
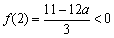
所以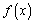
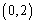
知识点
设
经长期观察，函数y=f（t）的图象可以近似地看成函数
正确答案
解析
略
知识点
设函数
（1）当
（2）讨论函数
正确答案
见解析
解析
知识点
定义在区间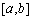
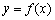
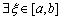
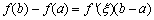
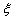
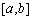
①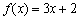
②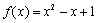
③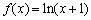
④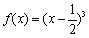
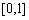
“中值点”多于一个的函数序号为____，（写出所有满足条件的函数的序号）
正确答案
①④
解析
略
知识点
有编号分别为1，2，3，4，5的5个红球和5个黑球，从中取出4个，则取出的编号互不相同的概率为（ ）
A
B
C
D
正确答案
解析
略
知识点
函数
A
B
C
D
正确答案
解析
略
知识点
设
正确答案
解析
因抛物线
知识点
若函数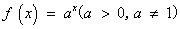
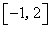
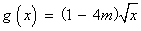
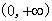
正确答案
解析
知识点
如果函数
A
B
C
D
正确答案
解析
略
知识点
下列函数中，在其定义域内既是奇函数又是增函数的是
A
B
C
D
正确答案
解析
略
知识点
扫码查看完整答案与解析