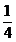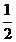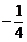- 函数的概念与基本初等函数
- 共5812题
已知函数

(1)求函数
(2) 





正确答案
见解析。
解析
(1)∵
∴.故函数



(2)解法一:

∵


由余弦定理得:


故

因为

解法二:

∵


由正弦定理得:

∵







知识点
16.已知函数


(1)求函数
(2)若函数





正确答案
见解析。
解析
解法一:(1)因为



所以



因为

所以

(2)由(1)知

因为

要使函数



因此实数

解法二:(1)同解法一。
(3)由(1)知

令

因此函数

令

因此函数

要使函数

只有


知识点
12.在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k丨n∈Z},k=0,1,2,3,4。给出如下四个结论:
①2011∈[1]
②-3∈[3];
③Z=[0]∪[1]∪[2]∪[3]∪[4]
④“整数a,b属于同一‘类’”的充要条件是“a-b∈[0]”。
其中,正确结论的个数是()
正确答案
解析
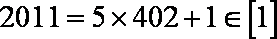
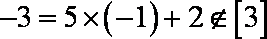
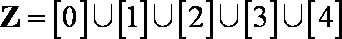
若整数
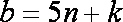
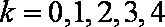
则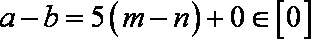
由以上,①,③,④正确,故选C。
知识点
21.已知函数
(1)讨论函数
(2)若对任意


正确答案
见解析。
解析
(1)由已知函数


① 



② 


当



当



(2)由已知

则

即
设



而


进而转化为

又设

当



当



∴当



从而

知识点
3.已知函数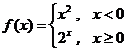
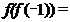
正确答案
解析
略。
知识点
8.若变量


正确答案
解析
本题考查的简单线性规划,如图,可知目标函数最大值和最小值分别为4和2。
故选B.
知识点
10.设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
正确答案
解析
f(x)是奇函数,g(x)是偶函数,∴|f(x)|为偶函数,|g(x)|为偶函数。
再根据两个奇函数的积是偶函数、两个偶函数的积还是偶函数、一个奇函数与一个偶函数的积是奇函数,可得 f(x)|g(x)|为奇函数,故选C。
知识点
13.将容量为n的样本中的数据分成6组,绘制频率分布直方图,若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频数之和等于27,则n等于()
正确答案
60
解析
设第一组至第六组数据的频率分别为2x,3x,4x,6x,4x,x,则2x+3x+4x+6x+4x+x=1,解得


故答案为60。
知识点
16.五位同学围成一圈依序循环报数,规定:①第一位同学首次报出的数为1,第二位同学首次报出的数也为1,之后每位同学所报出的数都是前两位同学所报出的数之和;②若报出的是3的倍数,则报该数的同学需拍手一次,当第30个数被报出时,五位同学拍手的总次数为 _________ 。
正确答案
7
解析
这个数列的变化规律是:从第三个数开始递增,且是前两项之和,那么有1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987
分别除以3得余数分别是1、1、2、0、2、2、1、0、1、1、2、0、2、2、1、0
由此可见余数的变化规律是按1、1、2、0、2、2、1、0
循环周期是8。
在这一个周期内第四个数和第八个数都是3的倍数,
所以在三个周期内共有6个报出的数是三的倍数,
后面6个报出的数中余数是1、1、2、0、2、2,只有一个是3的倍数,故3的倍数总共有7个,
也就是说拍手的总次数为7次。
故答案为:7。
知识点
15.已知函数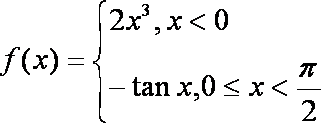

正确答案
-2
解析
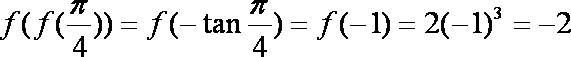
知识点
12.设E,F分别是Rt△ABC的斜边BC上的两个三等分点,已知AB=3,AC=6,则
正确答案
10
解析
由已知中E,F分别是Rt△ABC的斜边BC上的两个三等分点,已知AB=3,AC=6,我们可以以A为坐标原点,AB、AC方向为X,Y轴正方向建立坐标系,分别求出向量

以A为坐标原点,AB、AC方向为X,Y轴正方向建立坐标系
∵AB=3,AC=6,
则A(0,0),B(3,0),C(0,6)
又∵E,F分别是Rt△ABC的斜边BC上的两个三等分点,则E(2,2),F(1,4)
则


知识点
16.已知函数

(1)求
(2)若


正确答案
(1)
(2)
解析
(1)∵
(2)由


∵

∴
知识点
17.已知数列






(1)求

(2)若




正确答案
见解析。
解析
(1)∵



∴
∴

在



当




∴
∴

∴

知识点
5.已知△




正确答案
解析
由正弦定理得:






知识点
18.(本小题满分12分)已知函数
(Ⅰ)求
(Ⅱ)若




正确答案
见解析。
解析
(Ⅰ)∵

要使

从而△=

(Ⅱ)∵

∴

∴

∴



∵

∴

∴



知识点
扫码查看完整答案与解析