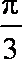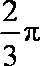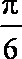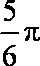- 函数的概念与基本初等函数
- 共5812题
4.某同学同时抛掷两颗骰子,得到的点数分别记为


正确答案
解析
由

知识点
5.下列函数中,既是偶函数,又在区间(0,3)内是增函数的是( )
正确答案
解析




知识点
10.已知变量



正确答案
解析
由题意作出其平面区域,
则x+2y≥﹣5恒成立可化为图象中的阴影部分在直线x+2y=﹣5的上方,
则实数a的取值范围为[﹣1,1].
故答案为:[﹣1,1].
知识点
8.已知函数y=f(x)是R上的偶函数,当x1,x2∈(0,+∞)时,都有(x1﹣x2)•[f(x1)﹣f(x2)]<0.设
正确答案
解析
根据已知条件便知f(x)在(0,+∞)上是减函数;
且f(a)=f(|a|),f(b)=f(|b|),f(c)=f(|c|);
|a|=lnπ>1,b=(lnπ)2>|a|,c=
∴f(c)>f(a)>f(b).
故选:C.
知识点
9.若把函数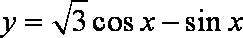
正确答案
解析
由题意知,
对称轴方程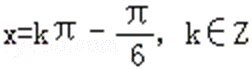

知识点
19.已知函数
(1)若
(2)若函数在
正确答案
(1)当

解析
(1)显然函数定义域为(0,+
令
当
当
(2)
令
当
当
故当

知识点
2.若角


正确答案
解析
因为角


所以
知识点
7.如图,网格纸上小正方形的边长为
正确答案
解析
由三视图可知,该多面体是一个四棱锥,且由一个顶点出发的三条侧棱两两垂直,长度都为4, ∴其体积为
知识点
8.已知函数






正确答案
解析
因为






知识点
22.在直角坐标系







(1)若直线


(2)设


正确答案
(1)
解析
(1)将曲线


直线


将








(2)曲线









知识点
15.设函数
正确答案
解析
由



【思路点拨】利用同底法求解指数、对数不等式.
知识点
已知x与y之间的一组数据:
则y与x的线性回归方程为y=bx+a必过点_________。
正确答案
(1.5,4)
解析
线性回归直线一定经过样本中心点
知识点
12.已知函数





正确答案
解析
若a=0则方程f(f(x))=0有无数个实根,不满足条件,
若a≠0,若f(f(x))=0,则f(x)=1,∵x>0时,f(
关于x的方程f(f(x))=0有且只有一个实数解,
故当x≤0时,a•ex=1无解,即ex=
故

知识点
16.如图所示,我舰在敌岛A南偏西50°相距12海里的B处,发现敌舰正由岛A沿北偏西10°的方向以每小时10海里的速度航行,我舰要用2小时在C处追上敌舰,则需要的速度是_______________.
正确答案
解析
略
知识点
21.已知二次函数


(1)如果


(2)如果
正确答案
见解析。
解析
(1)由




(2)由




即


知识点
扫码查看完整答案与解析