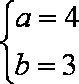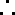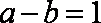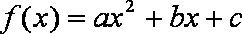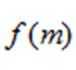- 函数的概念与基本初等函数
- 共5812题
11.若函数
正确答案
8
解析
知识点
21.已知
（1）讨论函数
（2）是否存在实数
（3）若方程
正确答案
见解析。
解析
（1）
（i）当a>0时，由ax2-1>0得 
故当a>0时，F(x)的递增区间为
（ii）当
（2）即使
（i）当a≤0时，由（1）知当
∴
（ii）当a>0时，由（1）可知
故存在这样的a的值，使得
a的取值范围是
（3）等价于方程
∵
所以 a的取值范围是
知识点
3.函数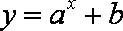
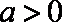
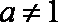
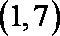
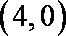
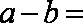
正确答案
1
解析
解析：由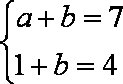
知识点
7.已知函数f（x）=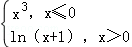
正确答案
解析
∵当x=0时，两个表达式对应的函数值都为零
∴函数的图象是一条连续的曲线
∵当x≤0时，函数f（x）=x3为增函数；当x＞0时，f（x）=ln（x+1）也是增函数
∴函数f（x）是定义在R上的增函数
因此，不等式f（2﹣x2）＞f（x）等价于2﹣x2＞x，
即x2+x﹣2＜0，解之得﹣2＜x＜1，
故选D。
知识点
8.以下判断正确的是（ ）
A命题“负数的平方是正数”不是全称命题
B命题“
C“a=1”是函数f（x）=cos2ax﹣sin2ax的最小正周期为π的必要不充分条件
D“b=0”是“函数f（x）=ax2+bx+c是偶函数”的充要条件
正确答案
解析
对于A，命题“负数的平方是正数”是全称命题，故A错误；
对于B，命题“
对于C，a=1时，函数f（x）=cos2x﹣sin2x=cos2x的最小正周期为T=
反之，若函数f（x）=cos2ax﹣sin2ax=cos2ax的最小正周期T=
所以“a=1”是函数f（x）=cos2ax﹣sin2ax的最小正周期为π的充分不必要条件，故C错误；
对于D，b=0时，函数f（﹣x）=ax2+bx+c=f（x），y=f（x）是偶函数，充分性成立；反之，若函数f（x）=ax2+bx+c是偶函数，f（﹣x）=f（x），解得a=0，即必要性成立；
所以“b=0”是“函数f（x）=ax2+bx+c是偶函数”的充要条件，故D正确．
故选：D.
知识点
14.设函数
正确答案
1
解析
作出
知识点
20.已知函数
(1)求
(2)当
正确答案
（1）
（2）
解析
(1)设点
于是有
所以，
(2)由(1)可知，
又
所以，
考察正弦函数
于是，
所以，当
知识点
2.函数
A
B
C
D
正确答案
解析
因为
知识点
10.函数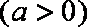
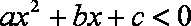
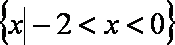
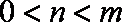
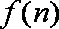
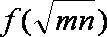
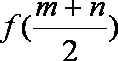
正确答案
解析
由已知得函数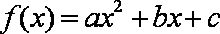
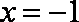
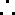
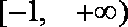
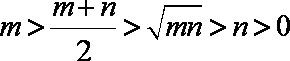
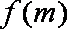
知识点
15.在空间中，下列命题正确的是( )．
A若两直线a,b与直线l所成的角相等，那么a∥b
B空间不同的三点
C如果直线l//平面
D若直线
正确答案
解析
考查直线，平面的位置关系，选D
知识点
16.（本题满分13分）已知函数f(x)＝(2cos2x－1)sin 2x＋
（1）求f(x)的最小正周期和最大值；
（2）当
正确答案
见解析。
解析
（1）因为f(x)＝(2cos2x－1)sin 2x＋
＝cos 2xsin 2x＋
＝
所以f(x)的最小正周期为
（2）因为f(α)＝
因为
所以
知识点
6.函数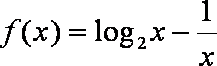
正确答案
解析
∵
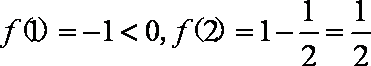
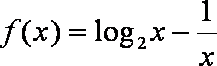
知识点
20.设函数f(x)＝
（1）求b，c的值；
（2）若a>0，求函数f(x)的单调区间；
（3）设函数g(x)＝f(x)＋2x，且g(x)在区间(－2，－1)内存在单调递减区间，求实数a的取值范围.
正确答案
见解析。
解析
（1）函数的定义域为(－∞，＋∞)，f′(x)＝x2－ax＋b，
由题意得
（2）由（1）得，f′(x)＝x2－ax＝x(x－a)(a>0)，
当x∈(－∞，0)时，f′(x)>0，当x∈(0，a)时，f′(x)<0，
当x∈(a，＋∞)时，f′(x)>0.
所以函数f(x)的单调递增区间为(－∞，0)，(a，＋∞)，单调递减区间为(0，a).
（3）g′(x)＝x2－ax＋2，
依题意，存在x∈(－2，－1)，使不等式g′(x)＝x2－ax＋2<0成立，
即x∈(－2，－1)时，
当且仅当“x＝
所以满足要求的a的取值范围是(－∞，－2
知识点
2.下列函数中，既是偶函数又在区间（0，+ ∞）上单调递减的是（ ）
A
B
C
D
正确答案
解析
知识点
4.某班全体学生参加口语测试，成绩的频率分布直方图如图，数据的分组依次为：[20，40)，[40，60)，[60，80)，[80，100].若低于60分的人数是15，则该班的学生人数是________.
正确答案
50
解析
由频率分布直方图，低于60分的频率为(0.01＋0.005)×20＝0.3.所以该班学生人数为
知识点
扫码查看完整答案与解析